


4.2 The Dark Matter Distribution From Giant Arcs
For most arcs observed in rich clusters and given in
Table 1,
the angular distance of the arc from the cluster center ranges between 10"
to 30". From Table 2 we see that the model
velocity dispersion is quite
compatible with the observed value deduced from spectroscopic
redshifts of galaxy members. The total mass within
the critical radius ranges between 1013 to 5 x
1014 M .
The mass-to-light ratio is about ~ 100 for the R filter, indeed in
good agreement with the classical dynamical mass
estimator (M/L ~ 250 from the virial mass or from the X-ray
analysis). The gravitational lens approach directly confirms that
clusters of galaxies are dominated by invisible
mass in the innermost regions where arcs are observed. But
the modeling of giant arcs also gives the matter distribution
on scales of
.
The mass-to-light ratio is about ~ 100 for the R filter, indeed in
good agreement with the classical dynamical mass
estimator (M/L ~ 250 from the virial mass or from the X-ray
analysis). The gravitational lens approach directly confirms that
clusters of galaxies are dominated by invisible
mass in the innermost regions where arcs are observed. But
the modeling of giant arcs also gives the matter distribution
on scales of  100
h50-1 kpc through the
various fitting techniques described above.
In this respect the modeling of MS2137-23 provides the first
spectacular results because of the existence of
a radial and a tangential arc
(Fort et al. 1992).
MS2137-23 is a demonstrative example of modeling with an elliptical potential.
The tangential and radial arcs are on the same side
with respect to the center of the cluster and they are necessarily
images of two different sources.
Furthermore, since the tangential arc does not show an
opposite counter arc, we are sure that a circular potential is
excluded.
Mellier, Fort, &
Kneib (1993)
modeled MS2137-23 with a non
singular elliptical potential. The uniqueness of the solution was shown by
the positions of 2 other images associated with the tangential arc and the
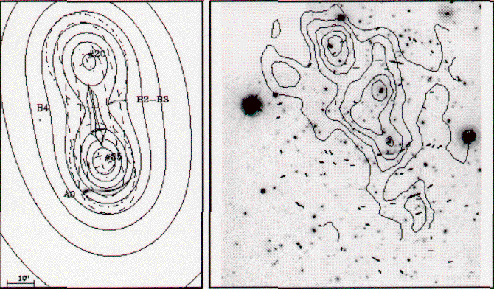
radial arc (Fig. 11). The model was able to
predict successfully the
position of the second image associated to the radial arc.
From the modeling, they found that the
cluster core radius is very small (30 h50-1
kpc), and that the dark
matter distribution has the same ellipticity and orientation as the
faint extended halo of the cD galaxy located at the center of the
cluster. The small core radius was indeed expected from the
position of the radial arc with respect to the cluster center, because it
should be close to the internal critical line
(Miralda-Escudé 1993a).
Therefore, the conclusion that the core radius of this X-ray cluster is
extremely small is direct and quite robust (see also
Miralda-Escudé
1994).
The total mass of MS2137-23
within the external critical line (given by the tangential arc) ranges
between 3 to 7 x 1013 M
100
h50-1 kpc through the
various fitting techniques described above.
In this respect the modeling of MS2137-23 provides the first
spectacular results because of the existence of
a radial and a tangential arc
(Fort et al. 1992).
MS2137-23 is a demonstrative example of modeling with an elliptical potential.
The tangential and radial arcs are on the same side
with respect to the center of the cluster and they are necessarily
images of two different sources.
Furthermore, since the tangential arc does not show an
opposite counter arc, we are sure that a circular potential is
excluded.
Mellier, Fort, &
Kneib (1993)
modeled MS2137-23 with a non
singular elliptical potential. The uniqueness of the solution was shown by
the positions of 2 other images associated with the tangential arc and the
radial arc (Fig. 11). The model was able to
predict successfully the
position of the second image associated to the radial arc.
From the modeling, they found that the
cluster core radius is very small (30 h50-1
kpc), and that the dark
matter distribution has the same ellipticity and orientation as the
faint extended halo of the cD galaxy located at the center of the
cluster. The small core radius was indeed expected from the
position of the radial arc with respect to the cluster center, because it
should be close to the internal critical line
(Miralda-Escudé 1993a).
Therefore, the conclusion that the core radius of this X-ray cluster is
extremely small is direct and quite robust (see also
Miralda-Escudé
1994).
The total mass of MS2137-23
within the external critical line (given by the tangential arc) ranges
between 3 to 7 x 1013 M depending on the source
redshifts derived from the color indices. This gives a M/L ratio
in the range 140 to 340.
The measurement of the arc redshifts in MS2137-23 should be a
priority for the very large telescopes.
depending on the source
redshifts derived from the color indices. This gives a M/L ratio
in the range 140 to 340.
The measurement of the arc redshifts in MS2137-23 should be a
priority for the very large telescopes.
It is important to note that MS2137-23 is dominated by a single cD galaxy. Apart from its high X-ray luminosity, MS2137-23 would not have been reported as a rich cluster candidate according to the richness criteria defined by Abell (number of detectable galaxy members within a 1 Mpc radius). But for most cluster lenses we observe a real correlation between the light distribution of galaxies or the X-ray emission, and the mass distribution, rather than between the number density of galaxies and the mass distribution (see A370: Fig. 12). This is observed even if a giant central cD is not yet formed (Cl2244 and Cl0024+1654). It will be important to test in the future if clumps of dark matter are regularly associated with the largest luminosity peaks and if it is still true at very large redshift. Note that the massive (very) distant dark halo detected in the field of the double QSO Q2345 already seems a possible counter example (Bonnet et al. 1993). It would be important to check if it is at least associated with an overdensity of faint blue galaxies.

|
| Figure 11. Modeling of the multiple arc system in MS2137-23 by Mellier et al. (1993). The tangential and radial arcs are visible on the CCD image (obtained at CFHT). Isocontours inferred from the modeling have been superimposed, as well as the predicted images. We see that the counter images are located on real objects in the field with the right elongation and orientation. Note that the surface brightness contours R = 26 arcsec-2 of the faint extended halo of the cD are compatible with the orientation and ellipticity of the potential. |
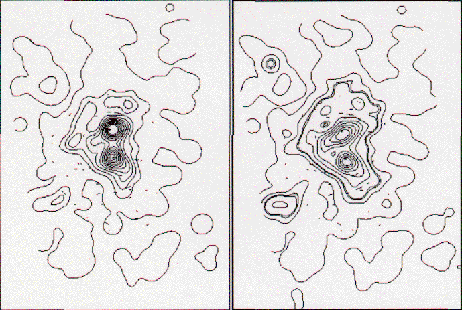
Similar modeling has been performed by Kneib et al. (1993) for A370 from new ultra-deep CCD images obtained at CFHT with exceptional seeing of 0.5". Within the giant arc itself are seen two breaks which are typical of a cusp arc. Kneib et al. (1993) also used gravitational pairs observed in the deep CCD images and demonstrated the double nature of the cluster potential. They also predicted the position of a third image associated with the brightest gravitational pair (see Fig. 1). The two potentials have again small core radii, and are centered on the two brightest galaxies with the same ellipticity and orientation as their luminous envelopes. Recent ROSAT/HRI observations definitely confirm that A370 is double (Böhringer, Mellier, Kneib & Briel, in preparation, and Fig. 12) with two density peaks located on the two brightest galaxies! Moreover, the distribution of arclets traces the overall geometry of the X-ray map and confirms that dark matter is associated with the brightest ellipticals of the cluster (Tyson et al. 1990, Fort 1992).
|
|
| Figure 12. Analysis of the the matter distribution in the cluster A370. The top right panel shows the red light distribution from the isoluminosity contours of galaxies. The top left panel shows the number density contours. The bottom right shows the blue CCD image of the clusters with the X-ray luminosity contours overlayed. On the three panels we superposed the arclets indicated by Fort (1992). The arclets directly show where the mass is located. In particular, we see that the arclet pattern indicates the presence of an extension toward the eastern region, which is also seen in the isoluminosity contours in the red-band and the X-ray maps. This clearly shows that in the center of this cluster light from galaxies and from the hot gas trace the mass. Note the arc reconstruction and the mass model in the fourth panel (the triplet B2-B3-B4 is discussed by Kneib et al. 1993 and in Fig. 1). The X-ray map confirms a posteriori that the predicted bi-modal shape of A370 by Kneib et al. (1993) was correct. The luminosity maps extend toward the south direction, and the X-ray map may have a secondary enhancement on the other side of A5. If it were confirmed, it would explain why A5 has a straight shape (cf Böhringer et al. 1994 for a more comprehensive discussion). |
MS2137-23 and A370 have shown that observations of several multiply lensed images with high spatial resolution can provide enough information to make predictive models. This is the observational path to follow but unfortunately only a few clusters have been observed with extremely deep CCD photometry and subarcsecond seeing. A2218 seems a good candidate because several arcs with redshifts have been detected (Pelló et al. 1992, Le Borgne et al. 1992) and some multiple images are suspected. The model is less constrained than MS2137-23 and A370, but gives basically similar results as MS2137-23 and A370 (Kneib et al. 1994), with a small core radius (< 30 h50-1 kpc), and a main deflector centered on the cD galaxy with the same orientation and ellipticity as its faint extended halo.
There is a real trend for arc-clusters dominated by giant galaxies to have a dark matter peak concentrated within 100 h50-1 kpc with an ellipticity and orientation similar to the faint stellar envelope of the giant galaxy at a surface brightness level of R = 26 (Fort et al 1992). However, the modeling of the inner part of the potential near the giant galaxies (inside the large arc radius) does not tell us if the model still holds at larger distances from the center. In particular the Mellier et al. (1993) modeling does not tell us if the cD halo can be identified with that of the cluster as a whole on Mpc scales. We cannot exclude a model with two components: one peaked (baryonic?) component linked to the giant galaxy superimposed on a shallower halo of Dark Matter on the cluster scale. This is a interesting point to investigate in future.
Hammer (1991) demonstrated that the thinness of arc(let)s favors peaked mass distribution models (see also Miralda-Escudé 1993a). Furthermore, if the dark matter is broadly distributed, the occurrence of arcs events should be considerably lower than is observed and the arcs should have much smaller axis ratios than are observed (Wu & Hammer 1993; Le Fèvre et al. 1994). The observed velocity dispersion of cluster galaxies in annuli at various distances from the center also helps to determine the profile of the potential. From this evidence, Hammer (1991) and Wu & Hammer (1993) claim that lensing models with a de Vaucouleurs's density profile at large distance are more likely than non singular isothermal model. Later, Wu (1993a) pointed out that due to large uncertainties in the determination of the observed velocity dispersion at various distances from the center it is still difficult to clearly separate the two models by statistical analyses. In this respect, if the distribution of Dark Matter on cluster scales is not too clumpy, the only hope of determining whether the potential fits a de Vaucouleurs law (whose physical meaning is still an enigma) will be to try to measure the weak shear at large radius from the center. The existence of a small core radius has been also found from the statistical analysis of the number of giant arc events compared with the number of arclets (Bergmann & Petrosian 1993), and now seems to be confirmed from a re-analysis of X-ray data for nearby rich clusters (Eyles et al. 1991; Gerbal et al. 1992; Briel, Henry & Böhringer 1992, Durret et al. 1994), although contradictory results were obtained during the last decade. Bartelmann & Weiss (1994) argued that the discrepancies between the core radii inferred from lensing and from X-ray observations in some rich clusters could be explained if the hot gas was expelled from the cluster members after the dark matter cluster potential was formed. They presented numerical simulations which give compact cores for the dark matter and a core twice as large for the hot gas distribution.
The statistical analysis of the arc(let)s around the two compact clusters A1689 and Cl1409 which have not yet formed a cD galaxy at their centers suggests that they have core radii smaller than 100 kpc (Tyson, Valdes & Wenk 1990). This result shows that the peaked mass density may be really associated with the cluster as a whole, and not only with a central cD. Some new data are available to investigate this problem. The modeling of Cl0024+1654, which has a clump of 4 bright elliptical galaxies at its center (Kassiola, Kovner & Fort, 1992), is possible with a single halo having a core radius ranging from 75 to 100 h50-1 kpc. Cl2244-02 (Fig. 13) has also a dense core of several bright ellipticals. It was modeled by Hammer et al. (1987), Kovner (1989), Hammer & Rigaut (1989), and Bergmann, Petrosian & Lynds (1990). They investigated a large range of models, but they do not give definitive evidence that the dark matter is strongly peaked, although systems with a concentrated mass distribution work. Recently Mellier (unpublished) succeeded in obtaining a modeling that fits the images of the large arc and possible counter-image candidates with a single peaked halo having a core radius of about 80 kpc. A beautiful new case of large arcs within a non-cD cluster has been reported in MS0440+02 by Luppino et al. (1993). For all of these cases it is of primary importance to get deep images with very high spatial resolution in order to find new multiple images, and to search for radial pairs that would constrain the core radius. Such observations are now scheduled with HST.
Arc(let)s have not been extensively used yet to study the clumpiness of the dark matter on intermediate scales and to reveal various mass concentrations in clusters. This was done for the modeling of A370 described above. In A2218, a second concentration of mass is needed to explain the second arc system around the second brightest member of the cluster. (see Pelló et al. 1992; Kneib et al. in preparation, and Fig. 14). Several of the straight arcs are simply understood by assuming that they are located on a saddle between two massive clumps. MS0302+17 is a typical example (Mathez et al. 1992). At least half of the cluster-lenses seem to be clumpy, which confirms that even the richest clusters are not completely relaxed gravitational systems.
| Cluster | Grav. images | rc
(h50-1 kpc) |  1D 1D km s-1 | 1014 M
(h50-1 M 
| M/LB (M  /L /L ) h50 ) h50
|
| A370-M1(1a,b) A370-M2(2) A370-M3(3) A370-M4(4) A370-M5(5) | Arc Arcs+Arl Arc Arc Arcs+Arl. | -  180 180
100 - 88-105 | - 1350 1100 900 820-850 | 2 .93 4.2 2 - | 130 190 400 100 - |
| C12244-M1(6) C12244-M2 (7) | Arc Arc | 6.33 ** < 110 | - 630 | 2 - | 140 - |
| A1689(8) | Arclets | 35-75 | 1200-1500 | - | - |
| C10024+17(9) | Arcs | < 110 |  1300 1300
|  1 1
| - |
| C11409+52(8) | Arclets | 35-75 | 1100-1500 | - | - |
| MS2137-23(10) | Arcs | 35-55 | 1250-950 | 0.3-0.7 | 340-140 |
| MS0302+17(11) | Arcs | 250 | 1100 | - | 140 |
| A2390-M1(12) A2390-M2(13) | Arc Arc | - 120-240 | 1250 1260 | 1.5 - | 120 100 |
| C10500-24(14) | Arc | - | < 1200 | < 1.8 | < 300 |
| AC114(15) | Images | < 170 | 770-1600 | - | - |
| A2218(16) | Images | 30 | 770-1000 | - | - |
| ** Effective radius of the de Vaucouleurs law. | |||||
(1a): Hammer (1987); (1b): Soucail et al. (1987): (2): Grossman & Narayan (1989); (3): Narasimha & Chitre (1988); (4): Mellier et al. (1990); (5): Kneib et al. (1993); (6): Hammer et al. (1989); (7): Mellier et al. (1994); (8): Tyson et al. (1990); (9): Kassiola et al. (1992); (10): Mellier et al. (1993); (11): Mathez et al. (1992); (12): Pelló et al. (1991); (13): Kassiola et al. (1992); (14): Wambsgnass et al. (1989); (15): Smail et al. (1994); (16) Kneib et al. (1994).