


4.1 Large Arcs and Central Potential
In Section 2 we showed that the location
and morphology of arcs provide
information on the projected mass distribution
within the corresponding critical line.
The relevant parameters for the modeling of the lens
are the position of the arcs with respect to a possible cluster center,
the number of merging images together with observed parity changes,
the break between each merging image
which gives the position of the critical line, the length and
width of arcs, the ratio of their curvature radius
and their distance from the center,
their orientation, and last but not least,
their redshifts. For a given geometry of the universe it is
necessary to scale the projected mass density by measuring the redshift
of at least one large arc. Only then can the total mass in the cone of light
delineated by the arc be determined. The mass can be well estimated
just by using a point mass lens M(r < rarc)  c2
r2 D / 4G. For larger
radii the total mass M(r) can be derived if the gradient of the
potential is known as a function of r. It will be seen
later that M(r) can be derived from
observations of the arclets. In fact it would be useful to get the redshifts
of several bright arc(let)s at various distances from the center, but the
probability of having two bright arc(let)s in the same cluster
is very small and no such cases have been observed yet.
c2
r2 D / 4G. For larger
radii the total mass M(r) can be derived if the gradient of the
potential is known as a function of r. It will be seen
later that M(r) can be derived from
observations of the arclets. In fact it would be useful to get the redshifts
of several bright arc(let)s at various distances from the center, but the
probability of having two bright arc(let)s in the same cluster
is very small and no such cases have been observed yet.
Miralda-Escudé (1993a) has summarized how some generic features of arcs can guide the modeling. As an example, for single elliptical potentials, a steep mass density profile generates thin arcs oriented along the minor axis of the potential. Similarly, a shallower potential profile generates thick arcs along the main axis (Kovner 1989). Consequently, the ratio between the curvature radius and the radial distance is small for steep potentials, whereas it is large for shallower potentials. The curvature and orientation of tangential arcs only provide an upper limit for the core radius for an elliptical potential (second order dependence, Kneib 1993). This poor dependence on core radius is quite understandable, since no rays of light are deflected in the very center of the cluster for large tangential arcs. Only multiply-lensed images with a radial arc (Fig. 11) give strong constraints on the typical scale of the mass profile since a radial arc is formed in the steepest part of the potential near the core radius (Miralda-Escudé 1993a). Finally, the shape of arcs, such as straight arcs (A2390, MS0302), or the position of peculiar merging images (A370), can suggest several mass concentrations that should be modeled with multiple potentials. Kovner (1989) gave numerous theoretical examples with two elliptical potentials that is a precious guide for a quick qualitative understanding of observers data.
In practice, the mass distribution in clusters is deduced by fitting the image produced by an analytic potential (or an analytic projected mass density) to the observations. Smooth circular or elliptical models with or without point mass distributions have been used: galaxy point masses in the very first models (Hammer 1987) with a fast image reconstruction method proposed by Schramm & Kayser (1987) and Kayser & Schramm(1988), nearly elliptical mass distributions (Grossman & Narayan, 1989; Narasimha & Chitre, 1988; Mirada-Escudé 1993a); halos following a de Vaucouleurs law (Hammer & Rigaud 1989; Angonin, Hammer & Le Fèvre 1992). It is worth noting here that Mellier & Mathez (1987) gave an approximate 3D mass density profile corresponding to the de Vaucouleurs law over five orders of magnitude, that is relatively easy to use for lens modeling:
The projected elliptical potential given in part 2 was
extensively used by
Kovner (1987a);
Mellier et
al. (1990);
Kochanek (1990);
Kassiola, Kovner &
Blandford (1992);
Mellier, Fort &
Kneib (1993);
Kneib et al. (1993)
but is only valid for small ellipticities. Recently,
Kassiola & Kovner
(1993a),
and
Kormann, Schneider
& Bartelmann (1994)
computed analytic expressions with pseudo-isothermal elliptic
mass distributions which are easily tractable and valid for large
ellipticities. In practice, with the image resolution
of ground based telescopes there
are almost no significant discrepancies
in the resulting matter distribution discussed
below when different analytical expressions
or fitting procedures are used. This will probably not be the case
with future arc images expected with the refurbished
Hubble Space Telescope.
So far, our knowledge of the distribution of
dark matter in distant clusters is rather indirect
and poor. Therefore, most of the models are chosen to be as
simple as possible with a minimum number of free parameters which
do not exceed the number of observational parameters. The simplest approach is
to verify if the single elliptical potential model described
in part 2 fits the images of
large arcs.
When arc images contain too few significant pixels
the reconstruction of the potential may be done using minimization
techniques with a priori hypotheses which are often not
based on observations. For instance, Kovner's models
(1988) minimized
the source size. The results were so convincing that they
immediately appeared as additional proof of the gravitational nature of
the newly discovered arcs. It can also be assumed that the
distant source has a circular shape. But more sophisticated
techniques can be used with images having high angular resolution.
Good examples are given by
Mellier, Fort &
Kneib (1993),
Kneib et
al. (1993), and
Miralda-Escudé (1994)
for modeling MS2137-23 and A370. These clusters are among the
most constrained because they show several multiple images.
Each image is defined by its position (Xi,
Yi), its
shape (ai,
The fitting procedure for the modeling of a potential can be described
as follows.
For a given set of potential parameters,
all the image segments of an arc system associated with a
(presumed) unique source are projected back to the source plane
(Fig. 10, bottom panel), and the
position and shape of the projected images are
considered together. Each image produces an individual object in the
source plane that the procedure attempts to superimpose perfectly
onto a single object of well-defined shape, by varying the potential
parameters. When a good fit is obtained,
the antecedent sources of each arc segment
must be very close to each other. Projected back to the image plane,
the source must generate at least as many images as
are observed (Fig. 10, bottom panel). It can also
give extra, eventually demagnified, images
that can or cannot be observed on the CCD images, but
which are crucial tests for any
modeling. Even if the minimization is done in
the source plane, we have to check the goodness of the fit in the image
plane by looking at the differences between the images generated by
the source in the model potential and the observed images.
It is actually better to optimize the reconstruction directly in the
image plane where we benefit from the magnification factor.
In general, the best
models are not unique but with the resolution of ground based telescopes
the family of solutions are similar whatever the optimization procedure
used. Nevertheless, for some exceptional cases
the observed number of gravitational images is large enough to
(over)constrain the elliptical model described in
part 2.4. For MS2137-23
and A370, the procedure has worked out so well that it
was even possible to predict the location of faint additional images
of arcs that have been detected a posteriori on deep CCD
images. The prediction capability of a lens modeling is the most convincing
way to prove the validity of a solution.
For future HST images
of arcs, the spatial resolution will be far higher than the
width of the arc (about one arcsec). One could use the
Etherington theorem (1933)
which prescribes that each corresponding
element of a multiple image has the same surface brightness as
its antecedent in the source plane.
Kochanek et
al. (1989)
successfully used this approach on some high resolution images of radio
rings (the so-called Ring-Cycle algorithm).
For exceptional optical images obtained with ground
based telescopes,
Kochanek & Narayan
(1992)
have extended the Ring-Cycle approach with
the lensclean algorithm which allows reconstruction of
the source.
This has not been done yet with real observations, but this is certainly
the next step for modeling giant optical arcs from
HST images.
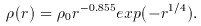
 i,
i,  i), and in some cases its redshift
(zi).
The image parameters depend on the intrinsic parameters of the source
but they also carry information about the lensing potential.
Kochanek (1990),
Miralda-Escudé (1991a), and
Kneib (1993)
defined some tractable estimators
which relate simply the source and image parameters to the potential.
Fig. 16
shows the relation between the shape parameters and the convergence and
the shear. The total number of direct
observational constraints is given by the number of multiple images.
Additional indirect
constraints are also used, such as the velocity dispersion of the
cluster galaxies, the position and shape parameters of the giant
central galaxies, and eventually X-ray maps. The center of the potential
that is derived from the arc(let)s pattern is in fact
a critical parameter for the modeling. When a huge cD galaxy is found at
the cluster center it often coincides in position with
the center of the potential, as inferred from lensing.
But in most of the cases given in table 1
there is an uncertainty of at least several arcsec.
i), and in some cases its redshift
(zi).
The image parameters depend on the intrinsic parameters of the source
but they also carry information about the lensing potential.
Kochanek (1990),
Miralda-Escudé (1991a), and
Kneib (1993)
defined some tractable estimators
which relate simply the source and image parameters to the potential.
Fig. 16
shows the relation between the shape parameters and the convergence and
the shear. The total number of direct
observational constraints is given by the number of multiple images.
Additional indirect
constraints are also used, such as the velocity dispersion of the
cluster galaxies, the position and shape parameters of the giant
central galaxies, and eventually X-ray maps. The center of the potential
that is derived from the arc(let)s pattern is in fact
a critical parameter for the modeling. When a huge cD galaxy is found at
the cluster center it often coincides in position with
the center of the potential, as inferred from lensing.
But in most of the cases given in table 1
there is an uncertainty of at least several arcsec.