


3.4. Fluctuations in the Distributions of Mass and the CBR
As noted in Sections 2.3 and
3.1, structure
formation on the scale of galaxies and larger is thought to have
been dominated by the gravitational growth of small departures
from homogeneity present in the very early universe. The nature
of the initial conditions is open because we do not have an
established theory of what the universe was doing before it was
expanding. We do have a consistency condition, that a single set
of initial values must match many observational constraints.
I discuss here second moments of the large-scale fluctuations in
the distributions of galaxies and the thermal cosmic background
radiation (the CBR).
It is sensible to try the simplest prescription for initial
conditions first. Most widely discussed is the adiabatic cold
dark matter (ACDM) model Joe Silk mentions in his introduction.
In the simplest case the universe is Einstein-de Sitter and the
density fluctuations are scale-invariant (the density contrast

 /
/ appearing on the Hubble length is independent
of time). This case tends to underpredict large-scale density
fluctuations; the problem is remedied by lowering H0 or
appearing on the Hubble length is independent
of time). This case tends to underpredict large-scale density
fluctuations; the problem is remedied by lowering H0 or
 m
(Blumenthal et
al. 1988;
Efstathiou et al. 1990).
(1)
The wanted value of H0 is below most estimates of this
parameter, so
the more commonly accepted interpretation is that
m
(Blumenthal et
al. 1988;
Efstathiou et al. 1990).
(1)
The wanted value of H0 is below most estimates of this
parameter, so
the more commonly accepted interpretation is that  m is less
than unity. This leads to the grade in line 2a. It depends on the model
for structure formation, of course.
m is less
than unity. This leads to the grade in line 2a. It depends on the model
for structure formation, of course.
Examples of second moments of the galaxy space distribution and the
angular distribution of the CBR are shown in
Figures 2 and 3.
The power spectrum of the space distribution is
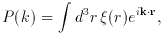 (13)
(13)
where the dimensionless galaxy two-point correlation function is
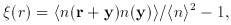 (14)
(14)
for the smoothed galaxy number density n(r). The data in
Figure 2 are from the IRAS PSC-z (point source
catalog) redshift survey
(Saunders et al. 1998)
of the far infrared-luminous galaxies mentioned in
Section 3.1. Since infrared
radiation is not strongly affected by dust this promises to be an
excellent probe of the large-scale galaxy distribution.
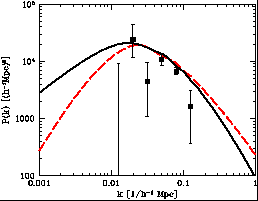
|
Figure 2. Mass fluctuation spectrum
extrapolated to
the present in linear perturbation theory for the ACDM model in
equation (17) (solid line, from
Tegmark 1998b)
and the ICDM model in equation (18) (dashed line). The
galaxy fluctuation spectrum is from the PSC-z collaboration
(Saunders et
al. 1998).
|
The expansion in spherical harmonics of the CBR temperature as a
function of direction in the sky is
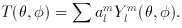 (15)
(15)
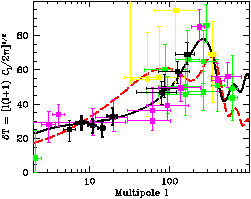
Figure 3 shows second moments of the expansion,
defined as
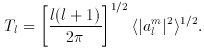 (16)
(16)
In the approximation of the sum over l as an integral
the variance of the CBR temperature per
logarithmic interval of l is
(Tl)2. The Tl data in
Figure 3 are
from the survey of the measurements by
Tegmark (1998a).
|
Figure 3. Spectrum of angular fluctuations of the
CBR. The data are from the compilation by
Tegmark (1998a).
The ACDM model prediction plotted as the solid line assumes the
parameters in equation (17)
(Tegmark 1998a).
The ICDM model prediction plotted as the dashed line assumes the
parameters in equation (18).
|
The solid curves in Figures 2 and
3 are the prediction
(Tegmark 1998a,
b)
of an ACDM model with a scale-invariant primeval mass
fluctuation spectrum and the parameters
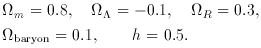 (17)
(17)
It is impressive to see how well this model fits the two sets of
measurements. But at the present accuracy of the measurements there is
at least one other viable model, shown as the dashed curves. It assumes
the same dynamical actors as in ACDM---cold
dark matter, baryons, the CBR, and three families of massless
neutrinos---but the isocurvature initial condition is that the
primeval mass density and the entropy per baryon are homogeneous,
and homogeneity is broken by an inhomogeneous primeval
distribution of the CDM. A simple model for the spectrum of
primeval CDM fluctuations is P (k)  km. A rough fit to the
measurements has parameters
km. A rough fit to the
measurements has parameters
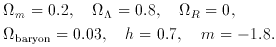 (18)
(18)
Further details and a pedigree within the inflation picture are in Peebles
(1999a,
b).
The solid curve fits the CBR anisotropy measurements
better, but it is based on a much more careful search of parameters to
fit the data. A bend in P (k) would do wonders for the dashed
curve.
Hu (1998)
gives another example of how the prediction of the CBR angular
fluction spectrum depends on the details of the structure formation
model.
As mentioned in Section 2.3, the point of
this discussion is that reading the
values of the cosmological parameters from the CBR anisotropy
measurements in Figure 3 is a dangerous
operation because it depends on
the theory for structure formation as well as the
Friedmann-Lemaître model. This
applies to other entries in category 2 in
Table 2 (and to line 1a: a
satisfactory quantitative understanding of galaxy formation would
include an understanding of the relation between the distributions of
galaxies and mass).
Our knowledge of P (k) and Tl will be
considerably improved by work in progress. Redshift surveys to
probe P (k) and the large-scale mass distribution include the
Century Survey, the Two Degree Field Survey (2dF), and the Sloan
Digital Sky Survey (SDSS); precision measurements of the CBR
include BOOMERANG, MAP, PLANCK, and other ground, balloon, and satellite
projects
(Geller et al. 1997;
Page 1997;
Nordberg & Smoot 1998;
Eisenstein et
al. 1998;
and references therein). If one of
the structure formation models now under discussion fits all the bumps
and wiggles in the measured spectra it will inspire confidence.
In the Einstein-de Sitter case a scale-invariant ACDM model normalized
by the assumption that galaxies trace mass gives quite a good fit to the
CBR angular fluctuation spectrum Tl; on this score it
would merit a
pass in line 2b. But the assumptions that galaxies trace mass and that
 m = 1 imply
quite unacceptable peculiar velocites. The situation
is different from line 1a, where the issue is whether
m = 1 imply
quite unacceptable peculiar velocites. The situation
is different from line 1a, where the issue is whether  m = 1 can
be saved by the postulate that galaxies do not trace mass. Thus I think
it is fair to give the Einstein-de Sitter case separate demerits in
lines 1a and 2b, but with a question mark for the latter because it
depends on the model for structure formation.
m = 1 can
be saved by the postulate that galaxies do not trace mass. Thus I think
it is fair to give the Einstein-de Sitter case separate demerits in
lines 1a and 2b, but with a question mark for the latter because it
depends on the model for structure formation.
Several authors have concluded that the low density flat ACDM model
(with  > 0) is a better fit
to the Tl measurements than is
the low density open case
(Gawiser & Silk 1998;
Tegmark 1998a).
Others note that other treatments of the still quite new
measurements can lead to the opposite conclusion
(Górski et
al. 1998;
Ratra 1998).
Since the former approach seems to treat the
measurements in the more literal way the flat case gets the higher grade
in line 2b.
> 0) is a better fit
to the Tl measurements than is
the low density open case
(Gawiser & Silk 1998;
Tegmark 1998a).
Others note that other treatments of the still quite new
measurements can lead to the opposite conclusion
(Górski et
al. 1998;
Ratra 1998).
Since the former approach seems to treat the
measurements in the more literal way the flat case gets the higher grade
in line 2b.
1 Lowering H0
or  m
lowers the expansion rate at the epoch of equality of mass densities in
matter and radiation, and the larger expansion time when the universe is
dominated by the pressure of the CBR increases the clustering length.
Back.
m
lowers the expansion rate at the epoch of equality of mass densities in
matter and radiation, and the larger expansion time when the universe is
dominated by the pressure of the CBR increases the clustering length.
Back.




 /
/ appearing on the Hubble length is independent
of time). This case tends to underpredict large-scale density
fluctuations; the problem is remedied by lowering H0 or
appearing on the Hubble length is independent
of time). This case tends to underpredict large-scale density
fluctuations; the problem is remedied by lowering H0 or
 m
(Blumenthal et
al. 1988;
Efstathiou et al. 1990).
(1)
The wanted value of H0 is below most estimates of this
parameter, so
the more commonly accepted interpretation is that
m
(Blumenthal et
al. 1988;
Efstathiou et al. 1990).
(1)
The wanted value of H0 is below most estimates of this
parameter, so
the more commonly accepted interpretation is that  m is less
than unity. This leads to the grade in line 2a. It depends on the model
for structure formation, of course.
m is less
than unity. This leads to the grade in line 2a. It depends on the model
for structure formation, of course.



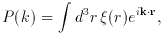
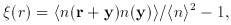

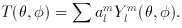
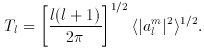

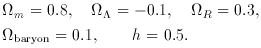
 km. A rough fit to the
measurements has parameters
km. A rough fit to the
measurements has parameters
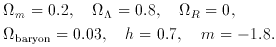
 > 0) is a better fit
to the Tl measurements than is
the low density open case
(
> 0) is a better fit
to the Tl measurements than is
the low density open case
(