3.5. The Evolution of Clusters of Galaxies

Bahcall and colleagues (Bahcall & Fan 1998 and references therein) have emphasized the importance of the time evolution of the number of clusters of galaxies as a probe of the cosmology. The condition that a CDM model fit the present cluster number density is (White, Efstathiou, & Frenk 1993; Bahcall & Fan 1998)

(19)

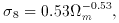
where ₈ = M/M is the rms contrast in the mass found within a randomly placed sphere of radius 8h^-1 Mpc. Since the rms fluctuation of galaxy counts is close to unity on this scale, ₈ (g) 1, equation (19) says galaxies trace mass if _m ~ 0.3, while biasing has to be substantial if _m = 1. I have already indicated why I am skeptical of the latter. More important, Bahcall & Fan (1998) demonstrate that with the Einstein-de Sitter parameters the ACDM model normalized to fit the present cluster number density quite underpredicts the abundance of clusters at z 0.5.

This result assumes Gaussian initial density fluctuations. If _m = 1 the present mass fraction in clusters is small, so the normalization is to a steeply falling part of the Gaussian. The time evolution of the rms density fluctuation consequently causes a large evolution in the predicted number of clusters. The Gaussian case is simple and natural to consider first, and it follows from simple models for inflation, but there are other possibilities. In the ICDM model (Section 3.4) the CDM could be a massive field squeezed from its ground level during inflation, in which cases the primeval CDM mass distribution is (r) = m² (r)² / 2, where is a random Gaussian process with zero mean. In this model the mass fluctuation distribution is much less steep than a Gaussian, the cluster abundance accordingly is a less sensitive function of the rms mass fluctuation, and the Einstein-de Sitter model predicts acceptable evolution of the cluster mass function (Peebles 1999b). It is not clear whether the constraint from the skewness of the galaxy count distribution (Gaztañaga & Fosalba 1998) allows the primeval mass fluctuations to be non-Gaussian enough for acceptable cluster evolution in the Einstein-de Sitter case.

The evolution of structure is a key probe of cosmology, and Bahcall and colleagues have demonstrated that the rich clusters of galaxies offer a particularly sensitive measure. But I am inclined to keep the question marks on the grades in line 2c until we can be more sure of the nature of the initial conditions for structure formation.