3.6. Cluster Baryon and Dark Matter Masses
This important probe was pioneered by White et al. (1993). In the survey by White & Fabian (1995) the ratio of the mass in X-ray emitting gas to the gravitational mass in rich clusters of galaxies is
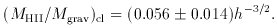
Myers et al. (1997)
find from the measurement of the
Sunyaev-Zeldovich effect in three clusters
In their contributions to this discussion Silk and Turner explain why
the consensus value of the density
parameter in baryons to account for light element abundances is
On the other hand, if baryons settled to cluster centers, increasing the
local ratio of baryon to total mass, it would bias this measure of
One does hears mention of the possibility of an inhomogeneous primeval
entropy per baryon, but with little enthusiasm.
As indicated in line 2d this constraint on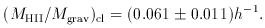
baryon = 0.02 /
h2. If clusters are fair samples
of baryon and total masses then baryon / m
is the same as (Mbaryon /
Mgrav)cl. If most
of the cluster baryons are in the plasma we get from these mass
ratios m =
(0.36 ± 0.09)h-1/2
and m = (0.33
± 0.06)h-1. The correction for baryons in
stars decreases m. Energy injected by winds from
supernovae in
cluster galaxies would tend to lower the plasma mass; a correction for
this effect would further lower m
(Metzler & Evrard
1998).
At h > 0.5 this measure of m is well below Einstein-de Sitter.
m low. It is
not hard to make up a story for how this might
have happened. Imagine that before there were clusters there were gas
clouds dense enough that the baryons dissipatively settled, leaving dark
matter halos. We have to postulate the clouds were small enough that the
radiation from this dissipative settling is not objectionably hard, and
we have to postulate that feedback from star formation prevented
catastrophic collapse of the baryons. Now imagine many of these systems
fall together to form a proto-cluster. Numerical N-body simulations of
merging show that the dense parts of the substructure tend to settle
relative to less dense parts, producing the wanted segregation of
baryons from the dark matter. Numerical simulations of cluster formation
fail to show any evidence of this story; I do not know whether that is
because it is only a story or possibly because it is hard to explore all
scenarios in numerical simulations.
m so far has proved difficult to finesse.