3. OUTSKIRTS OF THE GALAXY AND SUBMILLIMETER SPECTRUM

At low frequencies is also large ( -> 2 when 0-frequency isotropic conductivity dominates the dielectric tensor), so that the temperature changes only slowly with radius at the outskirts of the galaxy (~ 3 - 30 kpc) where the molecular gas distribution of galaxies rapidly becomes very patchy. The characteristic temperature at the outskirts of a typical galaxy would be ~ 30 - 50 K (see figure 1).

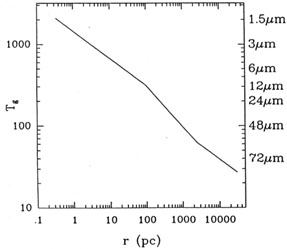
Figure 1. Temperature of directly illuminated 0.1 µm graphite grains as a function of distance from a central UV source of luminosity LUV = 1046 erg s-1. Planck-averaged absorption efficiencies used are from Draine & Lee 1984. For sources of other luminosities and grains of other sizes, the temperature in the flatter portions of the curve (T > 300 K, T < 60 K) scales roughly as (LUV / a)1/6, and in the steeper portion (60 K < T < 300 K) as (LUV / a)1/4. For a galaxy disk with a smooth logarithmic warp, dust at the given temperatures contributes predominately to the flux at wavelengths marked on the right.

A dust layer wil absorb UV flux incident at an angle to the normal of the layer if its column density > 10^-2 cos g cm^-2. With a Galactic gas-to-dust ratio spread over a disk of radius r_kpc this column corresponds to a mass of gas M_H 2 x 10⁸ cos r²_kpc M. The gas masses in nearby AGN are inferred from observations of CO (which of course depletion relates more directly to the dust than to M_H!) to be of order 10⁸-10¹⁰ M (Sanders, Scoville, & Soifer 1988a), and even in a young galaxy such as might surround a high redshift quasar it is unlikely that there would be more than ~ 10¹¹ M of processed gas. Consequently the disk will become optically thin beyond a few kpc (it could become thin at a smaller radius if most of the dust is clumped into clouds with >> 10^-2 cos g cm^-2, and such clouds at larger radii could preserve dust in neutral cores, but their covering factor would necessarily be very small).

Since the covering factor of dusty material at 20 K (~ 100 kpc) is expected to be very small, the spectrum of dust reradiation will be characterized by a rather well-defined minimum temperature, and should roll over sharply at wavelengths 200 µm with F ²⁺ at longer wavelengths (as for similar reasons it is observed to do in starburst galaxies and Galactic H II regions - cf. Telesco & Harper 1980). The precise form of the spectrum at 60 µm < < 200 µm will vary depending on the covering factor at large radius, which could be enhanced by the presence of companion galaxies (whose starlight maintains a minimum dust temperature ~ 20 K!), tidal tails, and the like.

As we discuss in section 5, at frequencies < 10¹¹ Hz, free-free emission from photoionized gas at the illuminated face of the disk will dominate the spectrum. Figure 2 shows the spectrum of continuum reradiation from gas and dust in an exponential disk with a logarithmic warp (d(covering factor) / d ln r = const). To illustrate how material at large radii can affect the far infrared and submillimeter spectrum, we show the effect of adding reradiation from a 2 x 20 kpc slab of dust extending from 10 to 30 kpc (which could represent a companion galaxy or a tidal tail).

Figure 2. Spectrum of reradiation from dust and photoionized gas in a warped disk surrounding a quasar with LUV = 1046 erg s-1. The solid line represents a disk containing 0.1 µm graphite dust having C = d(covering factor) / dln r = 0.1 exp(-r / 10kpc). Note the ``5 µm bump.'' The dot-dashed line shows the result of adding 0.03 to C for 10 < r < 30 kpc - representing a tidal tail or companion galaxy. The dashed line shows the spectrum of reradiation from (very large) grains assumed to radiate as black bodies, with the same covering factor distribution as for the solid line. The dotted line shows the contribution of free-free emission from the photoionized zones above the dust. There is no freedom in its normalization relative to the dust spectra.