


Between r ~ 1 kpc and the black hole's accretion disk proper
(r  103
GMh / c2 ~ 0.03 M8
pc for a black hole of mass Mh = 108
M8 M
103
GMh / c2 ~ 0.03 M8
pc for a black hole of mass Mh = 108
M8 M ) lies the
transition disk. Unlike the accretion disk, this disk will be heated
primarily by external radiation rather than by the local release of
gravitational binding energy. Beyond r ~ 20
) lies the
transition disk. Unlike the accretion disk, this disk will be heated
primarily by external radiation rather than by the local release of
gravitational binding energy. Beyond r ~ 20  2-2
M8 pc the stars in the
galaxy, of velocity dispersion 102
2-2
M8 pc the stars in the
galaxy, of velocity dispersion 102  2 km s-1
determine the potential. A
photoionized or molecular disk will be self-gravitating and Jeans
unstable if its column density exceeds
2 km s-1
determine the potential. A
photoionized or molecular disk will be self-gravitating and Jeans
unstable if its column density exceeds
where h is the scale height of the disk and T =
103 T3 K the gas
temperature. If this gas flows in on a timescale tin
to supply the black hole with an accretion rate
Since substantial warps are to be expected on all scales, we expect in
some average sense q 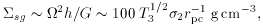
 =
= 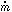 M
M yr-1, then
yr-1, then  ~ 1
~ 1
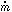 rpc-1 v300-1
(tin / torb)g cm-2 where
the orbital speed of the gas is 300 v300 km
s-1 and
torb is the orbital time of gas at radius
r. Purely local viscosity
results in enormous inflow times, and Begelman, Frank and Shlosman
(papers in these proceedings, and references therein) have argued that
the angular momentum transport is determined by self-gravitation and
global bar instabilities, so that the mean column density always
exceeds
rpc-1 v300-1
(tin / torb)g cm-2 where
the orbital speed of the gas is 300 v300 km
s-1 and
torb is the orbital time of gas at radius
r. Purely local viscosity
results in enormous inflow times, and Begelman, Frank and Shlosman
(papers in these proceedings, and references therein) have argued that
the angular momentum transport is determined by self-gravitation and
global bar instabilities, so that the mean column density always
exceeds  sg. Dust in
such a column has an enormous optical depth to UV
photons:
sg. Dust in
such a column has an enormous optical depth to UV
photons: 
 104
T31/2
104
T31/2  2 rpc-1. Provided
the disk is warped (by any of the
mechanisms described in section 2) or
flared, infrared reradiation is inevitable. A disk warped through angle
2 rpc-1. Provided
the disk is warped (by any of the
mechanisms described in section 2) or
flared, infrared reradiation is inevitable. A disk warped through angle
 will intercept and reradiate
a fraction ~
will intercept and reradiate
a fraction ~  / 3 of the
luminosity of the central source. For
idealized dust of constant
/ 3 of the
luminosity of the central source. For
idealized dust of constant  , if
C = d(covering factor) / dln r
, if
C = d(covering factor) / dln r
 rq,
then in the `inertial range' (kTmin << h<
rq,
then in the `inertial range' (kTmin << h< << kTmax) the superposition of
dust emission from all radii produces a reradiated spectrum with
L
<< kTmax) the superposition of
dust emission from all radii produces a reradiated spectrum with
L

 -s, where
-s, where
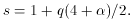
 0 and hence s ~ 1. A diversity of bumps and
wiggles is to be expected in individual objects, depending on the
radii (and hence, via figure 1,
wavelength) where their warps are most
pronounced, the size and composition of their dust grains, and whether
they are viewed from an angle where dust at a large radius absorbs
re-emission from the interior. This seems in accord with the infrared
spectral energy distributions of AGN: a great variety, with a median
s ~ 1
(Sanders et al. 1989,
1988b).
As discussed in section 2, the
properties of more realistic galactic dust modify slightly the simple
result of equation (4), and by flattening the T(r) relation introduces
a propensity for 3-5 µm ``bumps'' (see
figure 2).
0 and hence s ~ 1. A diversity of bumps and
wiggles is to be expected in individual objects, depending on the
radii (and hence, via figure 1,
wavelength) where their warps are most
pronounced, the size and composition of their dust grains, and whether
they are viewed from an angle where dust at a large radius absorbs
re-emission from the interior. This seems in accord with the infrared
spectral energy distributions of AGN: a great variety, with a median
s ~ 1
(Sanders et al. 1989,
1988b).
As discussed in section 2, the
properties of more realistic galactic dust modify slightly the simple
result of equation (4), and by flattening the T(r) relation introduces
a propensity for 3-5 µm ``bumps'' (see
figure 2).