Annu. Rev. Astron. Astrophys. 1992. 30: 653-703 Copyright © 1993 by Annual Reviews. All rights reserved

3.3.3 BALLOON OBSERVATIONS AT 19.2 GHZ A number of groups have undertaken balloon observations at centimeter, millimeter and submillimeter wavelengths to measure the anisotropy on scales 1-20° over the last decade. Some of these results have not yet been fully analyzed but preliminary results have been published.

Boughn and Cottingham and their collaborators have made observations on a series of balloon flights using a single conical horn antenna equipped with a ruby maser operating at 19.2 GHz with a bandwidth of 400 MHz (Cottingham 1987, Boughn et al 1990, 1991, 1992). The aim was to have a 3° beam, which would have required a 3 meter horn at this frequency - far too long for the required stability against wind on a balloon. The horn was therefore shortened to 0.9 meter and equipped with a polyethylene lens to flatten the wavefront. The antenna was rotated about the vertical axis at 1.5 rpm, and scanned a circle at constant zenith angle of 45°. A major objective of this program was to obtain an actual map of a large area of the sky. This dictated the single horn configuration, and the system was Dicke switched between the sky and a 4.3 K cold load. In dual-beam systems many linear drift terms can be eliminated to high precision with difference measurements, but these are not suitable for making actual images. In the present case, accurate sky maps were obtained, but the data first had to be corrected for offsets of ~ 0.1K and drifts of the order of 50 mk/hr. The response of the maser across the 400 MHz band varied by over 10dB and the effective bandpass was 210 MHz.

The first flight of the instrument was in May, 1986, from Palestine, Texas (Cottingham 1987). In these observations the Dicke switch frequency was 8 Hz. The resulting sky map was sufficiently sensitive (1.5 mK per 3 x 3° beam) to place the limit on anisotropy on scales from 3-25° given in Table 4.

This instrument has since been flown on another flight from Palestine, Texas, and two flights from Alice Springs, Australia (Boughn et al 1990). The data from the Alice Springs flights are not yet fully analyzed, but the data from the two Palestine flights have been analyzed (see Boughn et al. 1991, 1992).

Boughn et al calculated a model of the expected Galactic contribution from synchrotron radiation based on the 408 MHz map of Haslam et al (1982). In portions of the sky where they could compare this Galactic model with their observations they agreed only to within a factor two, which was probably due to a combination of systematic errors and spectral index variations over the frequency range 0.4-19 GHz. They subtracted the mean level and best-fit dipole and their calculated Galactic model from the data, and analyzed the residuals.

In view of the quantity of data it was not easy to apply the likelihood ratio test in the usual way. Boughn et al (1991) have therefore adopted an alternative approach in which they simulate the experiment plus the model they are testing in the following manner. They first assume a specific model which is described by the correlation function C() of the temperature, T, of the microwave background radiation. They define a statistic, S', given by:

(9)

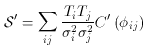
where _i and _j are the actual measurement errors for the different fields in their observations, C'() is the correlation function convolved with the antenna beam pattern and (_ij) is the angular separation of the positions corresponding to T_i and T_j. The statistic S' is not identical to the likelihood ratio statistic, S, but it is used in a similar way. A Monte Carlo analysis is used to generate the distribution of S' based on the distribution of the T_i given by C(). They then vary the value of the rms temperature fluctuations and so determine the distribution of S' for different levels of fluctuation. They next calculate the observed value of the statistic, S'_obs, given by Equation 9, where T_i, T_j are now observed temperatures after subtracting means and drift values. The value of S'_obs is then compared with the family of distributions of S'. A confidence level, 1-, is chosen and from the family of S' distributions one then selects that distribution, S', for which the probability of a greater value of S' is equal to . The rms fluctuations corresponding to this distribution, T_rms, provide the upper bound which is sought. Fluctuations with rms amplitude greater than T_rms have a probability < . We use ``'' because it is being used in the same way as the size in the likelihood-ratio test.

Boughn et al use this method not only to estimate upper limits on anisotropy as described in the preceding paragraph based on the actual measurements of T_i and T_j, but also to calculate the expected level of observed T fluctuations assuming that the rms variations due to the intrinsic microwave background radiation fluctuations are zero. In this ``null test'' the T<sub>i</sub> and T<sub>j</sub> generated in their Monte Carlo tests are due to instrumental noise alone. The median value of this distribution is then an estimate of the expected value of S' in the absence of fluctuations, and this value is used in place of S'<sub>obs</sub> to define the ``expected upper bound'' in the absence of intrinsic fluctuations. Corresponding values of T_rms are shown in Figure 4a, together with the limits based on the actual measurements. In these simulations they ran 100 or 200 Monte Carlo tests for the results shown in Figure 4a, and in Table 4, respectively. The scatter in different runs indicates that the uncertainties in these results due to the analysis statistics alone are ~ 10% and 5%, respectively. They adopt two forms for C(), or, equivalently, W(k) - monochromatic and Gaussian. Only the results for the Gaussian spectrum are given here.

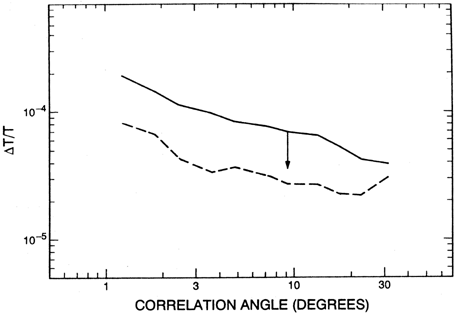
Figure 4a. Limits on the anisotropy set by Boughn et al (1991) at 19.2 GHz. The solid line indicates the 95% confidence upper limit as determined in a test similar to the likelihood ratio test, but using a slightly different statistic, with a Monte Carlo simulation assuming a Gaussian form for W(k) as described in the text. The dashed line indicates the level of sensitivity of the observations determined by the same method, but setting the fluctuations in the microwave background radiation to zero. It is clear that fluctuations have been detected over the whole range of angular scales from 1-30°. As in the case of the Davies et al result (Figure 3c), the detected anisotropy might all be due to Galactic synchrotron emission, but intrinsic microwave background radiation fluctuations at a level of T/T ~ 10-5 cannot be ruled out.

As can be seen in Figure 4a, the fluctuations in sky temperature are significantly larger than expected from the noise level in these observations. Thus it is clear that some anisotropy has been detected. Boughn et al ascribe this to Galactic synchrotron emission which has not been correctly accounted for based on the 408 MHz data and the extrapolation to 19.2 GHz and therefore interpret their observations in terms of upper limits, as shown in Table 4.