Copyright © 1993 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
653-703 Copyright © 1993 by Annual Reviews. All rights reserved |
3.3.4
In their first session the observations lasted for only 8.7 minutes
before a balloon failure aborted the experiment, but they were
nevertheless able to place interesting constraints on the anisotropy
(see
Table 4). The observations after
subtraction of the dipole term
are shown in Figure 3b.
In the second session the observations
lasted for ten hours. For the lowest frequency channel, after
correction for offsets and drifts, the best calibration was provided
by the dipole anisotropy of the microwave background radiation itself.
Meyer et al assumed a value for the dipole amplitude of 3.3 mK
[Lubin et al 1985;
D. A. Cottingham (private communication);
Smoot et al 1991b].
They allowed for one additive and one multiplicative parameter for
each one-hour segment of data, and two parameters for the direction of
the dipole, so that 6 hours of data was fitted with 14 parameters. A
map of about half the northern hemisphere was then made, and they then
excised the data with Galactic latitude |b| < 15° and analyzed
the residuals for anisotropy. The
Meyer et al assumed a Gaussian form for the spectrum W(k), and
followed the method of
Boughn et al (1991)
described above. A
statistic, S'obs, was again formed. Meyer et al assumed a
certain correlation angle,
Meyer et al considered the possible sources of this anisotropy,
apart from the microwave background radiation itself. The most likely
candidates are Galactic dust emission, quasi-stationary atmospheric
emission or systematic errors due to instrumental effects. They
pointed out that the expected level of Galactic dust emission,
Meyer et al
concluded that there was definitely some anisotropy at the
level  2 fit to the dipole term is
1.7 per degree of freedom, which shows that there is definitely excess
variance in these observations.
2 fit to the dipole term is
1.7 per degree of freedom, which shows that there is definitely excess
variance in these observations.
 c, and used Monte Carlo tests to
determine both the sensitivity of their observations using the null
statistic described above and the 95% confidence upper limits which
they could place on the microwave background radiation variations. In
their simulations they ran series of 300 Monte Carlo tests for a
number of values of
c, and used Monte Carlo tests to
determine both the sensitivity of their observations using the null
statistic described above and the 95% confidence upper limits which
they could place on the microwave background radiation variations. In
their simulations they ran series of 300 Monte Carlo tests for a
number of values of  c
covering the range 3-22°. The values
of
c
covering the range 3-22°. The values
of  T/T derived from the null
assumption and from their measured {
T/T derived from the null
assumption and from their measured { Ti} are shown in
Figure 4b. One can see immediately from
this figure that the
expected 95% confidence upper limit (indicated by the line) is
significantly below the 95% confidence upper limit derived from their
observations. The power of the tests for each upper limit derived is
greater than 90%. The fact that the 95% upper limits based on the
data are about a factor two higher than the expected 95% limits based
on the null assumption is clear evidence for excess variance.
Ti} are shown in
Figure 4b. One can see immediately from
this figure that the
expected 95% confidence upper limit (indicated by the line) is
significantly below the 95% confidence upper limit derived from their
observations. The power of the tests for each upper limit derived is
greater than 90%. The fact that the 95% upper limits based on the
data are about a factor two higher than the expected 95% limits based
on the null assumption is clear evidence for excess variance.
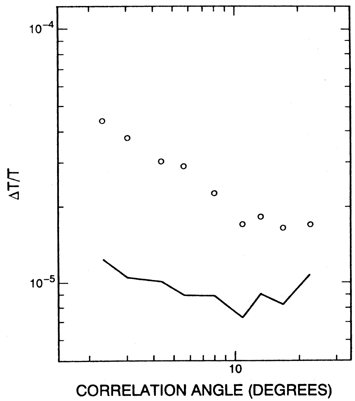
Figure 4b. Limits on the anisotropy set by
Meyer et al (1991a)
at 168 GHz.
The circles represent 95% confidence upper limits determined by the
same method as in
Figure 4a and assuming a
Gaussian form for
W(k), and the line represents the sensitivity of the observations,
determined from a Monte Carlo simulation in which the flucutaions due
to the microwave background radiation are set to zero. It is clear
that fluctuations have been detected over the whole range of angular
scales from 3-22°. The detected anisotropy might all
be attributable to Galactic thermal emission from dust, but intrinsic
microwave background radiation fluctuations at a level of  T/T
~ 10-5 cannot be ruled out.
T/T
~ 10-5 cannot be ruled out.
 T/T ~ 10-5, was
not far from their measured levels. Also, a
``stationary'' atmospheric cloud could have produced the excess, and
they did see clouds at high altitudes during part of their observing
time. Finally, their instrument could be susceptible to a number of
different effects, ranging from diffracted earthshine to magnetic
effects on their switches, but these were estimated to be
significantly smaller than the observed effect.
T/T ~ 10-5, was
not far from their measured levels. Also, a
``stationary'' atmospheric cloud could have produced the excess, and
they did see clouds at high altitudes during part of their observing
time. Finally, their instrument could be susceptible to a number of
different effects, ranging from diffracted earthshine to magnetic
effects on their switches, but these were estimated to be
significantly smaller than the observed effect.
 T/T = 1-3 x
10-5 on scales greater
than 4°, but that reasonable expectations of the level of
anisotropy in Galactic dust emission and in atmospheric emission were
close to this level and so could not be ruled out. They therefore
used their observations only to place upper limits on any intrinsic
anisotropy in the microwave background radiation.
T/T = 1-3 x
10-5 on scales greater
than 4°, but that reasonable expectations of the level of
anisotropy in Galactic dust emission and in atmospheric emission were
close to this level and so could not be ruled out. They therefore
used their observations only to place upper limits on any intrinsic
anisotropy in the microwave background radiation.