3.2. Modern K term

However, the problem with the K-term was even more serious because it was soon realized, via the non-existent Stebbins-Whitford (1948) effect and its explanation (Oke and Sandage 1968), that galaxy spectral energy distributions (SED) are very poorly approximated as black bodies, primarily because of the important 4000 ° break. Improvement of the SEDs that had been measured by Oke and Sandage was made by Whitford (1971). Oke and Sandage had observed only the central regions of five giant E galaxies using a spectrum scanner at the Cassegrain focui of both the Mount Wilson 60 and 100-inch reflectors. Whitford could observe a much larger fraction of the total E-galaxy light with his spectrum scanner at the Lick Crossley reflector because its shorter focal length and therefore smaller focal plane scale. The radial color gradient of E galaxies, becoming bluer from the center to the outside, explained the 10% difference between the two studies.

The resulting mean SEDs, shown in Fig. 2, permitted, for the first time, the calculation of realistic K(z) corrections for the effects of shifting the mean E-galaxy SED through various photometric pass bands. Since then, a large industry of K term calculations has developed, not only for E galaxies but for all Hubble types. A more modern history with entrance to the extensive literature is given elsewhere (Sandage 1988, 1995).

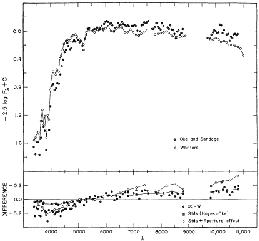
Figure 2. Mean spectral energy distribution of giant E galaxies as measured by Oke and Sandage (1968) for the very central regions and by Whitford (1971) for larger scanning apertures. These are the SEDs used for the first reliable calculation of the selective part of the K corrections in B, V, and R pass bands for E galaxies. The calculated K term in B using these SRDs was very much larger than the mpg K correction used by Hubble (1936b). Diagram from Whitford (1971).