1.4 The third dimension

When it became evident on the basis of the first measurements of galaxy redshifts by Slipher (1913) and others, a third dimension had become available for studies of galaxy distributions. De Sitter (1917) was the first to recognize that redshifts might be used as distance indicators, revealing the structure of the universe (Sect. 3.1.2).

In 1918 Writz gave an interpretation of the 15 redshifts available at this date (most of them obtained by Slipher):

``One can see from the values v of the spiral nebulae that they cannot be best represented by an apex direction and a velocity alone. The preponderance of one sign and the absolute size of the values show that a constant systematic error must be included in the least squares analysis...

Through the introduction of the constant k a considerable gain is achieved in the representation of the data...

It is remarkable that our system fixed stars should have such an incredibly large displacement of 820 km/sec, and equally strange is the interpretation of the systematic constant k = +656 km. If we give this value a literal interpretation it means that the system of spiral nebulae relative to the momentary position of the solar system as center disperses with a velocity of 656 km . . .

One will criticize the attempt made here to understand the characteristic arrangement and motion of the nebulae and argue, that everything is built on material which is much too incomplete and much too uncertain. True! Against this, however, I may hold two arguments, which are actually one. On the one side, experience shows again and again, that the law of large numbers arises already at remarkably small quantities of things, and then, W. Herschel deduced his apex of 1783 (with A = 262°, D = +26° for 1900) with only 13 stars . . .

. . . in the case of the nebulae, one may expect that we hold in our hands a fabric whose pattern we cannot yet unravel. One sees, however, in which direction observations have to be pushed forward in order to obtain the simplest description of the computational results connected with the nebulae.''

Application of the Doppler formula to the redshifts led to two velocity-distance relations originally derived by Wirtz (1922, 1924). One of them is reconstructed in Fig. 30. Galaxies could now be placed in velocity space and, with proper calibrations and corrections, in three-dimensional real space.

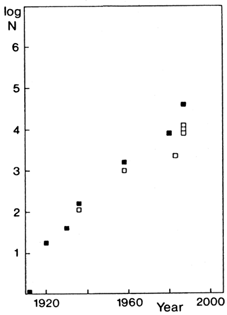
The progress in assembling redshifts z is slower than that of obtaining galaxy magnitudes and spherical positions. This is due to the loss of light in the spectrograph and the loss of light concentration through spectral dispersion. Processes which minimize this effect, e.g. the use of low-resolution objective prism spectra and redshift determination through colour measurements promise a much steeper increase in the number of measured redshifts for the future. Fig. 10 shows the rise up to now.

Figure 10. The increase in number of measured redshifts from 1912 to 1987. Open symbols: individual catalogues; filled symbols: cumulative data.

The first major step after the initial phase of redshift measurements (165 redshifts up to v = 42,000 km s^-1 by Hubble, 1936) was the presentation of more than 800 galaxy redshift measurements by Humason et al. (1956). The redshift catalogue assembled by Palumbo et al. (1983) lists a total of 8,250 galaxies with measured redshift, including 21 cm-redshifts, observed in various surveys until 1980.

A truly large-scale three-dimensional survey is the original CfA-survey (Huchra et al. 1983) with 2,400 redshifts up to m_pg = 14.5 and complete coverage of high galactic latitudes in the northern hemisphere. The southern extension of the CfA was recently completed (da Costa et at. 1988). The extension of the CfA to fainter magnitudes covers 117° x 6°, centered near the North Galactic Pole with objects from the Zwicky et al. (1961-1968) catalogue merged with data from the ESO-Uppsala catalogue (Nilson 1973) up to the limit m_B(0) = 15.5. The results for 1,100 galaxies have been published (de Lapparent et al. 1986), 7,500 redshifts were measured in 1987, a total of 15,000 redshifts is expected for the complete survey (Huchra 1988). A second extension was begun about 1985. It will cover 100° x 1° and reach m_B(0) = 17.5 (Geller et al. 1987). Still fainter surveys over tens of square degrees with modern multi-slit techniques are projected by different groups in both hemispheres.

Very low dispersion spectral surveys were started in Edinburgh and Cambridge and have shown that reliable methods for the determination of redshifts can be found, that the bulk of material, however, must be subjected to fully automatic procedures in order to get results from sufficiently large volumes of space. Algorithms to achieve this have recently been implemented by Schuecker (1988).

The use of colour measurements for the determination of redshifts was suggested by Zwicky (1959):

``It is only necessary to count the populations of the clusters [of galaxies] in various colour ranges C₁, C₂,. . ., C_k. One may for instance obtain photographs of a cluster in the colour range C₁ using a number of exposure times t_k. The ratios of the numbers of galaxies n (C₁, t_k) are then studied for different clusters. After certain calibrations, these ratios can give accurate information on the redshifts of extremely distant clusters whose characteristics cannot be studied by any of the methods proposed so far.''

Baum (1962) used measurements in different wavelength bands to derive cluster redshifts photometrically with relatively high accuracy. Several groups have adopted the method since. One such project is the determination of redshifts from CCDs taken with a set of interference filters by Loh (1988a, b) to obtain limits on q₀ and , and information on cluster evolution. A similar measuring method was discussed by Koo (1985).