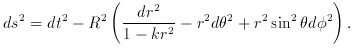3.1.2 Curvature and metric in general relativistic universes
The early relativistic world models are static.
Einstein (1917)
considered positive space curvature with matter acting as the
form-giving factor: the Einstein universe. When he found that his
solution was not stable he introduced a compensating factor, the
cosmological constant  (Sect. 3.2.4).
(Sect. 3.2.4).
De Sitter (1917)
found all three possible static solutions. For a
matter-filled universe it is the solution given by Einstein, the other
two solutions pertain to a universe without matter. Assuming  = 0, the
empty universe is Euclidean and corresponds to an Newtonian universe
or to an Einstein universe before the introduction of
= 0, the
empty universe is Euclidean and corresponds to an Newtonian universe
or to an Einstein universe before the introduction of  . A projection
of the Einsteinian universe into spaces of different curvature
requires that time be always and everywhere the same,
i.e. absolute. With
. A projection
of the Einsteinian universe into spaces of different curvature
requires that time be always and everywhere the same,
i.e. absolute. With 
 0 an empty universe of positive curvature can
be projected into a Euclidean or hyperbolic space under complete
invariance of all four variables.
0 an empty universe of positive curvature can
be projected into a Euclidean or hyperbolic space under complete
invariance of all four variables.
Observational evidence for a hyperbolical universe is discussed by de Sitter (1917) in the following:
``System A: time is the same everywhere and always, the time coordinate is different from the three space coordinates; system B: there is no universal time, no difference between coordinates in four-dimensional space, no physical meaning of the coordinates.
The three-dimensional space of this system of reference is the space with constant negative curvature, or hyperbolical space, or space of Lobatschewski.
In the system B the rays of light are straight lines in hyperbolic space . . . . In space B we have g44 = cos2. Consequently the frequency of light vibrations diminishes with increasing distance from the origin of co-ordinates. The lines in the spectra of very distant stars or nebulae must therefore be systematically displaced towards the red, giving rise to a spurious positive radial velocity . . . . Of the following three nebulae, the velocities have been determined by more than one observer:
Andromeda 3 observers - 311 km/sec. N.G.C. 1068 3 " + 925 " N.G.C. 4594 2 " + 1185 "
. . . . If, however, continued observations should confirm the fact that the spiral nebulae have systematically positive radial velocities, this would certainly be an indication to adopt the hypothesis B in preference of A.''
Friedmann (1922) introduced his metric as follows:
. . . . R is proportional to the curvature radius of space, which then may vary with time.
In the expression for the line element ds2 the terms g14, g24, g34 can be made to vanish for an appropriate choice of the time coordinate, or briefly speaking, time is orthogonal to space. For this second assumption, it seems to me, no physical or philosophical reasons can be given; it serves exclusively the purpose of making the computation simpler . . .
With the [above] assumptions ds2 can be brought into the form

whereby R is a function of x4 and M depends in the general case dependent on all four world coordinates.''
Friedmann then shows that both the Einstein universe and the de Sitter universe are special cases of his more general metric. The implicit assumption in Friedmann's metric is that the curvature is positive.
Two years later, Friedmann (1924) extended his models to negative curvature:
``. . . we can say that the stationary world with constant negative curvature of space is only possible with disappearing or negative density of matter....''
but
``. . . the possibility of non-stationary worlds with constant negative curvature of space and positive density [is given].''
Lemaître (1927) also allowed for both positive and negative curvature.
Tolman (1929) develops his metric with the two following conditions:
``As the first condition to be satisfied by the line element, we shall require it to be compatible for a limited region in space and time with the special theory of relativity
. . . As the second condition for the line element we shall require the possibility of writing it on a form which is spherically symmetrical in the spatial variables, symmetrical with respect to the past and future time, and static with respect to the time. These requirements, as is well known, lead necessarily to the form
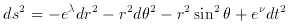
where
and
are functions of r alone. The requirement of spherical symmetry is an obvious one to impose, since otherwise the universe regarded on a large scale would have different properties in different directions. The requirement of symmetry with respect to past and future time means that the large-scale behaviour of the universe is reversible, and the static form of the line element means that by and large the universe is in a steady state.''
Robertson (1929) criticized Friedmann and Tolman on grounds of
``untenable assumptions . . . . instead of making full use of the intrinsic uniformity of such a space [homogeneous and isotropic] as we do here.''
His line element is:
where f is an arbitrary function of time.
While positive and negative curvature had been introduced into
expanding relativistic universes by 1924, the Euclidean universe - the
only one in Newtonian physics - was not considered until the work of
Heckmann, published in July 1931:
``The solutions of the Einstein field equations by Friedmann and
Lemaître frequently used in recent times, shall in the following be
extended. Especially the very simple proof shall be given that
besides the assumption of a spherical (or elliptical) closed space,
the assumption of a hyperbolical, in a limiting case even Euclidean
space, are of entirely equal standing within the framework of the
theory of relativity.''
It may be interesting to note, that de Sitter in a Harvard lecture
series given in October 1931 and published in 1932, discussed already
models of different values for
Figure 23. Four of Heckmann's nine models
of the universe
(Heckmann 1932).
Heckmann (1932)
published the full sequence of possible models with
three types of space curvature and three different signs of the
cosmological constant
``(1) has within the framework of the theory of relativity nine
different types of solutions, which originate from the combinations of
the three cases
where z is proportional to R,
where a, b, and
For the coordinates z and
Following Tolman and others,
Walker (1936)
published the now generally
used metric which includes the curvature parameter k:
Another consequence of Heckmann's paper was an immediately following
publication by Einstein and
de Sitter (1932)
describing the
relativistic Euclidean universe, the Einstein-de Sitter universe,
which was to become so important within the framework of the
inflationary universe
(Sect. 4.), opening with the sentence:
``In a recent note in the Göttinger Nachrichten,
Dr. O. Heckmann has
pointed out that the non-static solutions of the field equations of
the general theory of relativity with constant density do not
necessarily imply a positive curvature of three-dimensional space, but
that this curvature may also be negative or zero.''
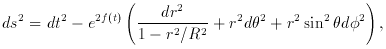
 and the three curvature parameters
and included a general sketch for three different cases (For a
forerunner of this type of diagram see
Sect. 3.1.3)
and the three curvature parameters
and included a general sketch for three different cases (For a
forerunner of this type of diagram see
Sect. 3.1.3)
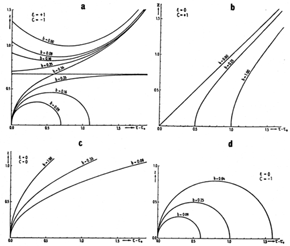
a ``This case is the richest. For M  0 it displays the de Sitter universe . . .'',
0 it displays the de Sitter universe . . .'',
b . . . . Except for vanishing matter term where the solutions become
straight lines intersecting the  -axis under 45°, all solutions rise
vertically from the
-axis under 45°, all solutions rise
vertically from the  -axis to
reach inclination 1 asymptotically . . . at infinity.''
-axis to
reach inclination 1 asymptotically . . . at infinity.''
c ``. . . With M  0 all solutions rise vertically from the
0 all solutions rise vertically from the
 -axis, their
inclination approaching 0 monotonously at infinity . . .''
-axis, their
inclination approaching 0 monotonously at infinity . . .''
d ``. . . for M  0 the solutions remain always finite and
(dz / d
0 the solutions remain always finite and
(dz / d )2 has a
zero z1, so that z = z1 is
envelope to the general solutions . . .''
)2 has a
zero z1, so that z = z1 is
envelope to the general solutions . . .''
 . All
models constitute solutions of the
differential equation
. All
models constitute solutions of the
differential equation
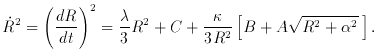
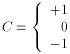 with the
three also possible
with the
three also possible  . These
types of solution shall be discussed in the following. The diagrams
included for illustration are computed for the special case of a
radiation-filled universe (A = 0). Though this case can only command
theoretical interest, it is nevertheless typical for the more general
cases A
. These
types of solution shall be discussed in the following. The diagrams
included for illustration are computed for the special case of a
radiation-filled universe (A = 0). Though this case can only command
theoretical interest, it is nevertheless typical for the more general
cases A  0; all characteristic
features appear in this model which,
however, has the great advantage that it can be expressed in
elementary functions . . .
0; all characteristic
features appear in this model which,
however, has the great advantage that it can be expressed in
elementary functions . . .
One can always give (1) the form
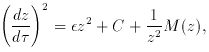
 proportional to t and
proportional to t and  assumes the values +1, 0, -1.
assumes the values +1, 0, -1.
M (z) is defined by
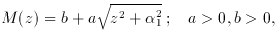
 1 are proportional to the corresponding constants A,
B, and
1 are proportional to the corresponding constants A,
B, and  in (1). C
is, as above, +1 for hyperbolic, 0 for Euclidean,
-1 for spherical metric.''
in (1). C
is, as above, +1 for hyperbolic, 0 for Euclidean,
-1 for spherical metric.''
 compare
de Sitter (1930),
Sect. 3.1.4. Note that the constant C
is the curvature parameter k,
except that the latter is positive for Euclidean and
negative for hyperbolical space.
compare
de Sitter (1930),
Sect. 3.1.4. Note that the constant C
is the curvature parameter k,
except that the latter is positive for Euclidean and
negative for hyperbolical space.