


3.1.3 Cosmic time
Time as one coordinate of the four-dimensional world was well established when Friedmann (1922) introduced the concept of the time-dependence of cosmic parameters, represented by the first and second time derivatives of the scale factors R (t), and thus the possibility of measuring cosmic time.
Well aware of the fact that the cosmological constant  cannot be
determined independently:
cannot be
determined independently:
``It should be remarked that the `cosmological' quantity
remains indetermined in our formulae'',
Friedmann considered solutions for t in a world of positive curvature
for different values of  . For
this he introduced the constant A,
which is directly proportional to the mass M of the universe, and
integrated his time-dependent form of Einstein's equations.
. For
this he introduced the constant A,
which is directly proportional to the mass M of the universe, and
integrated his time-dependent form of Einstein's equations.
Friedmann's ``monotonous world of the first kind'' is described as follows:
``The time of growth of R from 0 to R0 we will call the time since the creation of the world (5), this time t' is given by
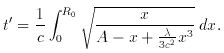
The time since the creation of the (monotonous) world (of the first kind) considered as function of R0, A,
has the following properties:
1. it grows with growing R0; it declines with increasing a, e.g., the mass in space decreases; 3. it decreases with increasing.''
Friedman's monotonous world of the second kind, for which it can also be shown that R is an increasing function of time, starts from
The ``periodic world'' requires that
``Our knowledge is completely insufficient to permit number computation
and to decide which world is ours . . . . With
The expansion age of the universe is given by the inverse Hubble
constant (defined below). The evolutionary age can be determined from
the evolutionary times of its oldest members plus the time from the
beginning of the universe to their formation. Two direct methods are
currently used:
- age of the oldest solid matter from our vicinity (meteorites, earth,
moon) from radioactive dating
- age of the oldest members of the galaxy (globular clusters).
The difference between the observed expansion age and the observed
physical age of the universe has plagued cosmologists almost from the
beginning.
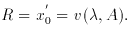
 lies within the limits (-
lies within the limits (- , 0),
with those values excluded which lead to more than infinite period.
, 0),
with those values excluded which lead to more than infinite period.
 = 0 and M = 5 x
1021 solar
masses, we find that the world period is of the order 10 billion
years. But these numbers can, of course, only serve as an
illustration for our computations.''
= 0 and M = 5 x
1021 solar
masses, we find that the world period is of the order 10 billion
years. But these numbers can, of course, only serve as an
illustration for our computations.''
5 ``The time since the creation of the world
is the time passed since the moment when space was a point (R =
0) to the present state (R = R0); this time may
also be infinite.'' Back.