


3.1.4 Look-back time
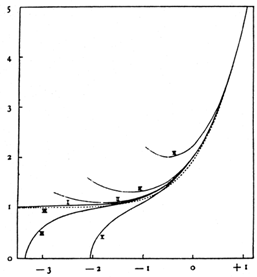
Figure 24, taken from
de Sitter (1930),
shows an early, probably the
first, diagram of the relation between world radius R, represented by
the dimensionless quantity z, and time t, represented by the
dimensionless quantity  -
-  0 (see
Sect. 3.1.1). De Sitter's definitions
are:
0 (see
Sect. 3.1.1). De Sitter's definitions
are:
and
with
With the appropriate choice of R0, e.g. the present
scale factor, an
infinite scale factor is reached asymptotically in a finite interval
Figure 24. ``Relation between z and
With reversed scales, taking again the present for reference, one
finds that R approaches 0 asymptotically in a finite interval
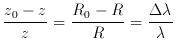
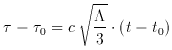
 = wavelength of
radiation
= wavelength of
radiation
 = Lemaitre's
cosmological constant in unit length-2,
= Lemaitre's
cosmological constant in unit length-2,
the subscript 0 indicates a fixed time.
 -
-  0, corresponding to infinite time, provided that
the cosmological
constant is a function of time (see
Sect. 3.2.4). The curves labeled
I-VII represent different world models.
0, corresponding to infinite time, provided that
the cosmological
constant is a function of time (see
Sect. 3.2.4). The curves labeled
I-VII represent different world models.
 -
-  0. The vertical coordinate is z, the
horizontal coordinate is
0. The vertical coordinate is z, the
horizontal coordinate is  -
-  0.''
(de Sitter 1930)
0.''
(de Sitter 1930)
 -
-  0. In this form the diagram displays the
look-back time for
various models. Different scaling permits to display the past
behaviour of different models in the form that is frequently used
today (e.g.
Tinsley 1968).
0. In this form the diagram displays the
look-back time for
various models. Different scaling permits to display the past
behaviour of different models in the form that is frequently used
today (e.g.
Tinsley 1968).