


3.2.2 Horizons
Schwarzschild (1916) derived a special solution to the original Einstein equations. The Schwarzschild metric has the line element
with
Eddington (1924)
showed that the introduction of the cosmological
constant led to an extended factor
in the line element and thus to a second horizon, the `world horizon'.
Different usage of the term horizon made standardization desirable. It
was provided by
Rindler (1956).
``We shall define a horizon as a frontier between things observable and
things unobservable. (The vague term thing is here used
deliberately).
There are then two quite different horizon concepts in cosmology which
satisfy our definition and to which cosmologists have at different
times devoted their attention. The first, which I shall call an
event-horizon, is exemplified by the de Sitter model-universe. It may
be defined as follows: An event-horizon, for a given fundamental
observer A, is a (hyper-) surface in space-time which divides all
events into two non-empty classes: those that have been, are or will
be observable by A, and those that are forever outside A's Possible
Powers of observation . . . .
The other type of horizon, which I shall call a
particle-horizon
(8), is
exemplified by the Einstein-de Sitter model-universe. It may be
defined as follows: A particle-horizon, for any given fundamental
observer A and cosmic instant t0 is a surface in
the instantaneous
3-space t = t0 to, which divides all fundamental
particles into two
non-empty classes: Those that have already been observable by A at
time t0 and those that have not.''
Fig. 27 gives an illustration of horizons.
Figure 27. Light-paths in a
model-universe (similar to a
Friedmann-Lemaitre model) possessing both a particle horizon and an
event-horizon
(Rindler 1956):
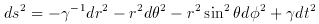
 = 1 - (2m
/ r).
= 1 - (2m
/ r).
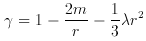
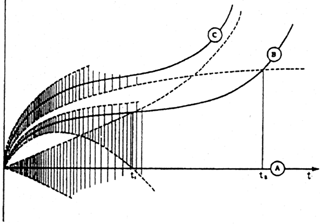
``The origin-observer is denoted by A. B is an observer on a typical
particle which becomes visible to A at creation-time
t1 (when A and B
enter each other's creation-light-cones) and which passes beyond A's
event-horizon at time t2, so that events at B after
t2 are outside A's
possible powers of observation. C is the critical particle which
becomes visible to A only at t =  . C's creation-light-track towards A
is that of the unique photon which reaches A at t =
. C's creation-light-track towards A
is that of the unique photon which reaches A at t =  , and which we have
already identified with A's event-horizon. And in the same way that A
approaches asymptotically the boundary of C's creation-light-cone, so
C approaches that of A's creation-light-cone. Evidently all particles
beyond C are entirely outside A's cognizance. In the diagram only the
positions near the vertices of the creation-light-cones have been
shaded in. We may note that the existence of a critical particle with
properties analogous to those of C above, one on each line of vision
of each fundamental observer, is a general feature of all models
possessing both types of horizon.''
, and which we have
already identified with A's event-horizon. And in the same way that A
approaches asymptotically the boundary of C's creation-light-cone, so
C approaches that of A's creation-light-cone. Evidently all particles
beyond C are entirely outside A's cognizance. In the diagram only the
positions near the vertices of the creation-light-cones have been
shaded in. We may note that the existence of a critical particle with
properties analogous to those of C above, one on each line of vision
of each fundamental observer, is a general feature of all models
possessing both types of horizon.''
8 ``It will be understood that whenever we
speak of particles in this context we always mean fundamental particles,
i.e. the representations of the nebulae in the world-model.''
Back.