


3.2 Basic parameters
3.2.1 R (t) - the scale factor, and its time derivatives
Friedmann (1922) has shown that in a non-stationary world Einstein's field equations, which tie geometry and matter together, relate the time-dependent scale factor R (t) and its first and second derivative to the mass density in the universe, the constant of gravity, the velocity of light and the cosmological constant. His equations
with
assume implicitly that the pressure p is zero. Later, these equations
were extended to include negative and null curvature
(Sect. 3.1.2).
Lemaître (1927)
formulated the time dependence of the field:
``Space is homogeneous and has constant positive curvature; space-time
is also homogeneous, for all events are perfectly equivalent. But the
partition of space-time into space and time disturbs the homogeneity.
The co-ordinates used introduce a centre. A particle at rest at the
centre of space described a geodesic in the universe; a particle at
rest otherwhere than at the centre does not describe a geodesic. The
co-ordinates chosen destroy the homogeneity of the universe and
produce the paradoxical results which appear at the so-called
`horizon' of the centre. When we use co-ordinates and corresponding
partition of space and time of such a kind as to preserve the
homogeneity of the universe, the field is found to be no longer
static: the universe becomes of the same form as that of Einstein,
with a radius no longer constant but varying with the time according
to a particular law.''
After introducing R as a function of time and its first and second
derivatives, Lemaître arrives at the same expression for the field
equations as Friedmann, including, however, the pressure term
where
``The four identities giving the expression of the conservation of
momentum and of energy reduce to
which is the energy equation. This equation can replace [the above
equation]. As V =
showing that the variation of total energy plus the work done by
radiation-pressure in the dilatation of the universe is equal to
zero.''
He summarized:
``It remains to find the cause of the expansion of the universe. We
have seen that the pressure of radiation does work during the
expansion. This seems to suggest that the expansion has been set up
by the radiation itself. In a static universe light emitted by matter
travels round space, comes back to its starting-point, and accumulates
indefinitely. It seems that this may be the origin of the velocity of
expansion
The search for a relation between the expansion of the universe and
energy available was continued by
Lemaître (1931b).
Another three
years later, he offered a new physical explanation for the expansion
(Sect. 4.1).
In his 1927 paper he also introduced the relation between redshift and
variation of the scale factor:
``The relation between radial velocity (redshift) is also given:
is the apparent Doppler effect due to variation of the radius of the
universe. It equals the ratio of the radii of the universe at the
instants of observation and emission diminished by unity.''
Later it became evident that the first derivative measured in units of
R is the increment H in the Hubble diagram or the Hubble
parameter
while the second derivative measured in units of H2 is the
acceleration parameter q. The symbols
were introduced by
Robertson (1955) and
Hoyle and Sandage
(1956),
respectively. The present values
(6) are H0 and
q0.
An attempt to measure the curvature radius of space was first made by
Schwarzschild
(1900):
``The question shall be discussed how large the curvature radius must
at least be chosen . . . For both cases the elliptical and the
hyperbolical space we will now discuss the problem of parallax
determination.''
The method using parallaxes was employed not only by Schwarzschild but
also, in the early-days of relativistic cosmology, by
de Sitter (1917).
In a more general way
the method is still the only one available. It is essentially the
measurement of a three-dimensional geometrical figure projected onto
the surface of four-dimensional space.
The area of the figure relates to the volume of a geodesic sphere and
thus to its radius of curvature. The result is obtained through model
fitting, so that the figure must be determined theoretically for
comparison.
For space with a time-dependent scale factor, the relation between
observational and theoretical quantities has been discussed in detail
by Heckmann (1942).
His photometric distance is
with R = scale factor at the time of observation
For small redshifts D is equal to the usual photometric distance.
Distance r should be compared to the spatial distance defined by
Whittaker (1931):
``The spatial distance of two material particles in a general
Riemannian space-time may then be thought of as a relation between two
world-points which are on the same null geodesic. It is obviously
right that 'spatial distance' should exist only between points which
are on the same null geodesic; for it is only then that the particles
are in direct physical relation with each other. This statement brings
out into sharp relief the contrast between `spatial distance and
`interval' defined by
for between points on the same null geodesic, the `interval' is always
zero. Thus 'spatial distance exists when, and only when, the
`interval' is zero.''
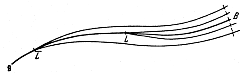
A symbolic presentation is given in
Fig. 25 taken from
Heckmann (1942).
Figure 25. Light path on a geodesic
(Heckmann 1942).
z is directly related to the Hubble parameter H, the deceleration
parameter q and the cosmological constant
For models with
Figure 26.
Mattig's (1958)
presentation of magnitude correction
A recent revival of the idea of measuring the Riemann curvature k /
R2
in a universe with
7 Series expansions were used at least
since 1931 (Lemaître) to relate observable quantities and
cosmological parameters. Heckmann's presentation is particularly
transparent because H and q appear explicitly.
Back.
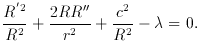
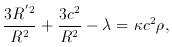
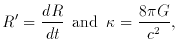
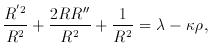
 is again given by
Einstein's expression. Lemaître continued:
is again given by
Einstein's expression. Lemaître continued:
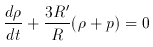
 2
R3, it can be written as
2
R3, it can be written as
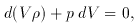
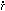 / R which
Einstein assumed to be zero and which in our
interpretation is observed as the radial velocity of extra-galactic
nebulae.''
/ R which
Einstein assumed to be zero and which in our
interpretation is observed as the radial velocity of extra-galactic
nebulae.''
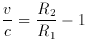
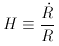
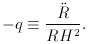
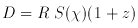
 ) = distance r.
) = distance r.
``Concerning the dependence of the apparent magnitude of a light source
from its position on the space geodesic which connects it to the
observer.''
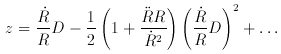
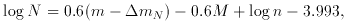
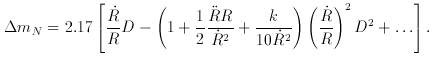
 .
.  mN is related to the
`angular' correction of magnitude m for distant objects.
mN is related to the
`angular' correction of magnitude m for distant objects.  mz is the
luminosity correction.
mz is the
luminosity correction.
 = 0 the
dependence of apparent magnitude m on H0,
q0 and z was given by
Mattig (1958,
Fig. 26).
= 0 the
dependence of apparent magnitude m on H0,
q0 and z was given by
Mattig (1958,
Fig. 26).
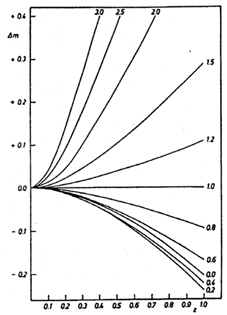
 m as
function of z and q0.
m as
function of z and q0.
 = 0 or
= 0 or
 is due to
Ehlers and Rindler
(1987).
Through a combination of m (z) and N (m)
measurements, the numerical values of the cosmological parameters can be
determined, as is apparent from Heckmann's equations.
is due to
Ehlers and Rindler
(1987).
Through a combination of m (z) and N (m)
measurements, the numerical values of the cosmological parameters can be
determined, as is apparent from Heckmann's equations.
6 Index 0 was introduced by
Friedmann (1922).
Back.