© CAMBRIDGE UNIVERSITY PRESS 1999

5. CLUSTER MASSES

The masses of clusters of galaxies within a given radius, M( r), can be determined from three independent methods:

a) Optical: galaxy velocity dispersion (and distribution) assuming hydrostatic equilibrium (Section 3.3);

b) X-Rays: hot gas temperature (and distribution) assuming hydrostatic equilibrium (Section 3.3);

c) Lensing: gravitational distortions of background galaxies (Tyson et al. 1990, 1996; Kaiser and Squires 1993). This method determines directly the surface mass overdensity.

The first two methods were discussed in Sections 2 and 3; the last (and newest) method is discussed in this book by Narayan. (See also Tyson et al. 1990, 1996; Kaiser and Squires 1993; Smail et al. 1995, and references therein).

The galaxy and hot gas methods yield cluster masses that are consistent with each other as discussed in Section 3 (with ²_r kT/µm_p). Gravitational lensing results, which provide direct information about cluster masses, are available only for a small number of clusters so far (with data rapidly increasing). For all but one of the clusters the masses determined from lensing are consistent, within the uncertainties, with the masses determined from the galaxies and hot gas methods (see Bahcall 1995 for a summary). Some differences in masses between the different methods are expected for individual clusters due to anisotropic velocities, cluster orientation (yielding larger lensing surface mass densities for clusters elongated in the line-of-sight, and vice versa), and sub-structure in clusters. On average, however, all three independent methods yield cluster masses that are consistent with each other. This triple check on cluster masses provides strong support for the important cluster mass determinations.

The masses of rich clusters range from ~ 10¹⁴ to ~ 10¹⁵h^-1 M within 1.5h^-1 Mpc radius of the cluster center. When normalized by the cluster luminosity, a robust mass-to-light ratio is determined for nearby clusters, with only small variations from cluster to cluster (Section 2.10)

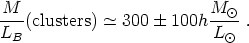
(49)

This result is similar to the one obtained from the baryon fraction in Section 4.

If, as desired by theoretical arguments, the universe has critical mass density _m = 1, than most of the mass in the universe cannot be associated with galaxies, groups, and clusters; the mass distribution in this case would be strongly biased (i.e., mass does not follow light, with the mass distributed considerably more diffusely than the light).