7. STELLAR NUCLEOSYNTHESIS: _* AND |Z|

The bolometric flux of the EBL derived in Section 6.1 is a record of the total energy produced in stellar nucleosynthesis in the universe, and so can be used to constrain estimates of the baryonic mass which has been processed through stars. The relationship between processed mass and background flux depends strongly on the redshift dependence of star formation and on the stellar IMF, but is only weakly dependent on the assumed cosmology for the reasons discussed in Section 4.2 and Section 5.

As an illustrative case, we can obtain a simple estimate of the total mass processed by stars by assuming that all stars formed in a single burst at an effective redshift z_e, and that all the energy from that burst was emitted instantaneously. The assumption of instantaneous emission does not strongly affect the result because most of the light from a stellar population is emitted by hot, short-lived stars in the first ~ 10 Myr. The integrated EBL at z = 0 in Equation 1 then simplifies to

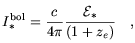
(6)

in which _* is the bolometric energy density from stellar nucleosynthesis and (1 + z_e) compensates for energy lost to cosmic expansion. In the case of instantaneous formation and emission, _* can be expressed in terms of the total energy released in the nucleosynthesis of He and heavier elements:

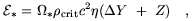
(7)

in which (~ 0.0075) is the mean conversion efficiency of energy released in nuclear reactions and Y and Z are the mass fractions of ⁴He and metals. Inverting Equation 6, the total baryonic mass processed through stars in this model can be derived from a measurement of the bolometric EBL using the expression:

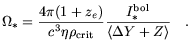
(8)

We can bracket a reasonable range for <Y + Z> by assuming the solar value as a lower limit, and the mass weighted average of the metal conversion fraction in E/S0 and spirals galaxies as the upper limit. ⁽³⁾ Assuming a 3:2 ratio of E/S0 to Sabc galaxies (Persic & Salucci 1992), we find <Y + Z> = 0.25±0.15. For z_e = 1.5, the total baryonic mass processed through stars corresponding to a bolometric EBL of 100±20 nW m^-2sr^-1 is then _* = 0.0030(±0.0019)h^-2 in units of the critical density, or 0.16(± 0.10)_B for _B = 0.019(± 0.001)h^-2 (Burles & Tytler 1998). Again, this calculation assumes a single redshift for star formation with all energy radiated instantaneously at the redshift of formation.

The true history of star formation is obviously quite different from this illustrative case. For time-dependent emission and formation, the bolometric EBL is the integral of the comoving luminosity density corresponding to realistic age- and redshift-dependent emission (see Equation 1). For comparison, instantaneous formation at the same redshift assumed above (z_e = 1.5) with a modified Salpeter IMF and time-dependent emission based on SEDs from Buzzoni (1995) would imply _* = 0.0037(± 0.0007)h^-2 for our estimate of the bolometric EBL (for details see MPD98 and Madau & Pozzetti 1999, MP99). The mean of this estimate is about 20% higher than that from the instantaneous formation and emission model discussed above. The two models are very similar because the vast majority of energy from a stellar population is emitted in the first ~ 10 Myrs. The quoted uncertainty is smaller than for our illustrative model because the error range reflects only the uncertainty in our estimate of the bolometric EBL and no uncertainties in the adopted IMF.

For the same IMF and SEDs, a redshift-dependent star formation rate for 0 < z < 4 based on the observed UV luminosity density and taking dust obscuration into account (see Steidel et al. 1999) would imply that almost twice as much mass is processed through stars than in the instantaneous formation model above (MP99). Relative to the instantaneous-formation models, the same bolometric EBL flux corresponds to a larger value of _* when we consider time-dependent star formation because more of the emission occurs at higher redshifts, resulting in greater energy losses to cosmic expansion. For our estimate of I^bol_EBL and the calculations of MP99 discussed above, we therefore estimate that total mass fraction processed through stars is _* = 0.0062(± 0.0012)h^-2 or 0.33± 0.07_B. We adopt this value for the remainder of the paper.

For this value of the total processed mass, we can calculate the corresponding metal mass which is produced in stellar nucleosynthesis. To do so requires an estimate of the metal yield - the mass fraction of metals returned to the ISM relative to the mass remaining in stars and stellar remnants. Best estimates of the metal yield, y_Z, lie between 0.01 (corresponding to a Scalo IMF) and 0.034 (as observed in the Galactic bulge) (Pagel 1987, 1999). These values incorporate the full range predicted by IMF models and observations (see Woosley & Weaver 1995; Tsujimoto et al. 1995; Pagel & Tautviaisiene 1997; Pagel 1997). For Z = 0.017 (Grevesse, Noels, & Sauval 1996), this metal yield range in solar units is y_Z = 1.3± 0.7 Z. If the mass fraction remaining in stars and stellar remnants is f, then the predicted metal mass density is given by

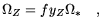
(9)

which gives _Z = 0.0040(± 0.0022)h^-2 Z, or _Z = 0.24(± 0.13) Z _B, for an assumed lock-up fraction of f = 0.5.

Note that we have assumed that the full flux of the EBL is due to stellar nucleosynthesis in the above calculations of _* and _Z. If 10h nW m^-2sr^-1 of the IR EBL is due to AGN, as estimated in Section 6.2, then the energy emitted by stars is smaller by about about 7%, and the inferred mass fractions are then smaller by about 7% as well.

³ Solar values of Y and Z are 0.04 and 0.02, implying DY/DZ = 2. Interstellar absorption measurements of DY/DZ in the solar neighborhood are closer to the range 3-4, implying Y ~ 0.07. Helium white dwarfs contribute an additional 10% of the local stellar mass to the estimate of Y (Fleming, Liebert & Green 1986), so that we have <Y + Z> = 0.07 + 0.02 + 0.1 ~ 0.2 as a local estimate for systems with solar metallicity. This is similar to estimates for other local spiral galaxies. Estimates for E/S0 galaxies are as high as 0.5 (Pagel 1997). (Note that the He mass produced in stars is written as Y to distinguish it from the total He mass, which includes a primordial component.) Back.