Annu. Rev. Astron. Astrophys. 1988. 26: 509-560 Copyright © 1988 by Annual Reviews. All rights reserved

2. DEFINITION

2.1. Luminosity Function and Density Function

Let (M, x, y, z) denote the number of galaxies lying in volume dV at (x, y, z) that have absolute magnitudes between M and M + dM. On the assumption that galaxian magnitudes are not correlated with spatial location, one can write

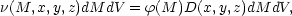
(8)

where

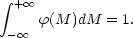
(9)

(M) gives the fraction of galaxies per unit magnitude having absolute magnitudes in the interval (M, M + dM) and is called the luminosity function. D(x, y, z) gives the number of galaxies (of all magnitudes) per unit volume at (x, y, z) and is called the density function. and D should be viewed as probability densities, which in practice are approached and represented either by (nonparametric) histograms or by (parametric) analytical forms.

If Equation 8 is valid for a sufficiently large portion of the Universe, or for sufficiently many samples of galaxies, (M) can be called the universal luminosity function of galaxies. This is clearly an approximation. In reality one expects that does somehow depend on the location, i.e. on the environment from which the galaxies are sampled. The question of universality of (M) is discussed in Section 4.3ff. Systematic differences of (M) with respect to type and environment, which are discussed in Sections 5 and 6, lead us to reject universality in the above sense; Equation 8 is subsequently revised in Section 6.3.

The present definition of the luminosity function of galaxies, as expressed by Equations 8 and 9, is identical to that used in stellar statistics (von der Pahlen 1937, Mihalas & Binney 1981). It should be noted that the conventional definition of the galaxian (M)) was different during the previous decades. The usual ("classical") method to determine the luminosity function of field galaxies (outside of rich clusters) was based on the assumption that D(x, y, r) = <D> = constant (see Section 3.2), which allows the product (M) ^. <D> to be discussed as one function; ever since van den Bergh (1961) and Kiang (1961), this product has been tagged with the label "luminosity function (M)," most recently in the review of Felten (1985).

Consequently the "luminosity function" has been given the units of density (number of galaxies per magnitude per cubic megaparsec). The drawback of this definition is the creation of an artificial dichotomy between field and cluster samples. Clusters of galaxies, where D constant is obvious, could strictly not have a luminosity function. In order to distinguish the function (M) <D> from (M), Schechter (1976) has introduced for the latter the term "luminosity distribution." Starting with Sandage et al. (1979) and Kirshner et al. (1979), the assumption that D = constant for field galaxies has been dropped. The general inhomogeneity of the distribution of galaxies is now widely acknowledged, and all new methods used to derive the luminosity function of field galaxies aim at a clear separation of and D (see Section 3.2, Table 1). A redefinition of (M) along the lines of stellar statistics (Equations 1, 2) is therefore most desirable at present. The mean density D, averaged over a significant portion of the observable universe, remains of course a most important quantity for cosmology, but there is no reason why it should be built into the luminosity function (provided that the notion of a universal shape for (M) makes any sense at all). The discussion of D is consequently left out of the present review.

The normalization of (M) to unity by integrating over all magnitudes (Equation 9) is difficult in practice because any sample of galaxies is complete, or has good statistical weight, only to a certain limiting magnitude M_lim. The ideal case, where the faint end of (M) goes to zero at a magnitude M' M_lim is at present applicable only to certain types of galaxies that are sampled nearby (cf. Section 5). In general, not only is nonzero but is growing exponentially at M_lim, making such a normalization infeasible; any extrapolation of (M) to fainter magnitudes by an analytical model will diverge. A way to avoid this divergence would be to go to the luminosity (L) representation of the luminosity function, transforming (M) into (L) and setting

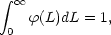
(10)

which for physical reasons must always converge. However, we wish to keep the magnitude representation, since (M) is closer to the observations than is (L). An obvious and practicable way to normalize (M) is to restrict the discussion to galaxies brighter than a certain arbitrary absolute magnitude 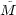, in which case Equation 9 is replaced by

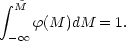
(11)

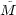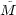D in Equation 8 is then the density of galaxies that are brighter than . may be different for different samples. Future work will push 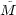toward fainter and fainter limits until the ideal normalization of Equation 9 can be realized.

It should be noted that the normalization is not a principal problem for the present concept. A normalization of (M) is needed only for the discussion of the density function D, which, by virtue of the adopted separation, is not a subject of this review. [Densities are only discussed where they have fundamental consequences for (M), such as in the context of the morphology-density relation (see Section 6).] For the discussion of (M) alone, no normalization is required because it is a probability distribution. Therefore, any (M), whether normalized or not, is called here a luminosity function. The luminosity functions of different samples can then be compared by their shape (i.e. the shape is the luminosity function). What matters only is that (M) is decoupled from the density function.

(M) is sometimes called the differential luminosity function, which should be distinguished from the integrated (or cumulative) luminosity function (M), defined as

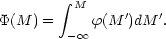
(12)

(M) is less frequently used than (M); it tends to conceal an intuitive interpretation of the information available for the fainter galaxies. In what follows, unless otherwise stated, LF is always meant to designate the differential luminosity function (M).