Annu. Rev. Astron. Astrophys. 1988. 26: 509-560 Copyright © 1988 by Annual Reviews. All rights reserved

3.2. Field Galaxies

The determination of (M) for field galaxies requires a well-defined sample whose bias properties are known. Almost always the samples are defined by an apparent magnitude cutoff m_lim. Unfortunately, existing galaxy catalogs are at best complete to a cutoff magnitude, which is not corrected for the direction-dependent Galactic absorption (e.g. Kiang 1976). But even to this limit, catalogs are incomplete for other reasons. The problem of low-surface-brightness galaxies has been discussed already in Section 2. Moreover, it is typical for flux-limited samples to become progressively more incomplete as the nominal value of m_lim is approached and to contain also, owing to magnitude errors, some fainter objects. The completeness of a catalog can be improved by adding missing objects from other sources (Kiang 1961). Alternatively, the incompleteness of a catalog can be compensated statistically by weighting each catalog entry with the magnitude-dependent incompleteness function; this function can be found by comparing the catalog under consideration with a deeper catalog, and it can be represented by an analytic distribution function (Sandage et al. 1979) of the type first used to describe -particle range straggling (i.e. a degraded half-step function on the trailing edge, often called the Fermi-Dirac function). An elegant way to test and to correct for incompleteness is supplied by the V / V_max technique, originally devised for quasars (Schmidt 1968) and subsequently extended to Markarian (field) galaxies by Huchra & Sargent (1973). Here V is the sample volume between the galaxy and the observer, and V_max is the volume the galaxy could lie in without dropping below m_lim [i.e. V_max = V(M) from below]. A sample is complete at magnitude m if the average V / V_max, calculated for all galaxies with magnitude m, is 0.5 if D = constant.

The absolute magnitudes of the sample galaxies must be calculated prior to the derivation of the LF. This requires distance information for every sample galaxy. The distance of field galaxies (except for very nearby ones) must be inferred from the redshift z, since no other precise method is available for all galaxy types.

For Friedmann models, the redshift in combination with H₀ and q₀ provides the luminosity distance (Sandage 1961, 1988). For small redshifts (cz 60, 000 km s^-1) the linear relation between the recession velocity v = cz and H₀ can be used without errors of more than ~ 0.2 mag as a result of neglect of space curvature between models with q₀ of 0 and 1. For large redshifts (i.e. z 0.5) the absolute magnitude normalization does depend on q₀ (Yee & Green 1987). Observed velocities must be reduced to the centroid of the Local Group (e.g. Humason et al. 1956, Yahil et al. 1977, Richter et al. 1987). The resulting corrected velocities v₀ still carry random peculiar motions v, which, however, are smaller than v 90 km s^-1 for field galaxies within v₀ < 500 km s^-1 (Tammann et al. 1980, Richter et al. 1987). A random velocity of v / v₀ 0.15 is a generous upper limit for any field galaxy; even this value would cause a random error in absolute magnitude of 0.3 mag at most and hence would broaden and flatten the LF only slightly. More serious are streaming motions of field galaxies. A Virgo-centric infall of v_VC = 220 km s^-1 at the circle of the Local Group has a noticeable influence on the LF of field galaxies within the Virgo complex (Kennicutt 1982, Kraan-Korteweg et al. 1984). Velocity and absolute magnitude corrections have been conveniently tabulated for a self-consistent Virgo-centric infall model by Kraan-Korteweg (1986). Some effect on the LF of field galaxies with 2000 v₀ 7000 km s^-1 is also to be expected from the apex motion toward the Hydra or Centaurus cluster at v₀ 4400 km s^-1 (Tammann & Sandage 1985, Lynden-Bell et al. 1987). In any case, the absolute magnitudes that are derived from velocity distances may still carry small direction-dependent errors within spheres surrounding the Virgo complex until our motion toward the microwave-background (MWB) dipole is fully understood. The size of such errors, if they exist, will be less than ±0.5 mag.

The specific choice of H₀ is irrelevant as long as only the shape of the LF is sought. However, if absolute magnitudes from velocity distances are mixed with those from directly determined distances (e.g. for Local Group members), the correct value of H₀ must, of course, be used. If LFs from different authors are compared, an adjustment for different adopted values of H₀ is necessary.

With the absolute magnitudes known, the next step is to construct (M). Table 2 is an overview of the various methods that have been used to derive (M) for field galaxies. It gives the references for each method and also shows whether (M) is derived in a parametric or nonparametric way and what assumptions are made about the density function D(x, y, z). The column "(M) parametric" divides the LFs into those that have and have not been represented by an a priori analytical expression. If "yes" is indicated, the Schechter parameters and M^* have been determined. "D = D(r)" indicates that spherical symmetry around the observer has been assumed. Because this assumption is unrealistic for the field in general, it implies that a restriction of the sample to a small solid angle of sky should have been made. Methods that were originally developed for the LF of quasars but that could in principle be applied also to field galaxies, are included in the present discussion. It is important to recall again that all methods fundamentally assume (M) to be independent of D (cf. Equation 8).

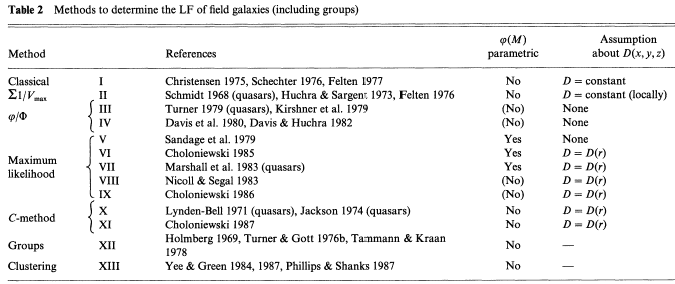
Five basic methods, or families of methods, can be distinguished in Table 2.

3.2.1    THE CLASSICAL METHOD    Until 10 years ago there was but one method to determine (M) for field galaxies; this is now called the classical method. Its basis is the assumption that galaxies are uniformly distributed in space (D = constant). Developers and early users of the method are van den Bergh (1961), Kiang (1961), and Shapiro (1971). These authors, however, did not describe the method. Detailed recipes for the construction of (M) in the classical way are given by Christensen (1975), Schechter (1976), and Felten (1977). At the heart of the method lies the calculation of the volume V(M) that is effectively surveyed for galaxies of absolute magnitude M. V(M) is determined by the maximum distance an object of absolute magnitude M can have and still be in the sample. The sample is limited by a fixed apparent magnitude m_lim, but this limit should be corrected for the direction-dependent Galactic absorption (Kiang 1976), with the excluded volume accounted for. The numbers of galaxies in bins of (M - 1/2 M, M + 1/2 M) must then be divided individually by V(M), giving a binned, nonparametric (M). At faint absolute magnitudes the number of sample galaxies per bin is decreasing because the surveyed volume for them is very small owing to the bright apparent magnitude m compared with the faint absolute magnitude M sought, making (m - M) very small. This is the reason that (M) becomes increasingly uncertain at faint M, to the point where it becomes meaningless. This is inherent to every LF study of field galaxies from magnitude-limited samples.

For the derivation of (M), Huchra & Sargent (1973) have used the V / V_lmax method. Instead of having the number of galaxies in bin (M - 1/2 M, M + 1/2 M) divided by V(M) = V_max, (M) is estimated by the sum (1 / V_max) over all galaxies in (M - 1/2 M, M + 1/2 M). Felten (1976) has shown that the two procedures are equivalent.

3.2.2    THE / METHOD    As galaxies of different absolute magnitudes are sampled in different volumes, any spatial inhomogeneity in the distribution of galaxies will severely distort (M) if it is constructed in the classical way with the assumption of homogeneity. For instance, a local density enhancement would overestimate (M) for absolutely faint galaxies, which are sampled only nearby. The danger is real because of the excess of nearby galaxies in the northern sky (known already to John Herschel). But only as the general inhomogeneity of extragalactic space became obvious with the advent of appropriate redshift samples (RSA, Davis et al. 1982) has the assumption of homogeneity been dropped. [To acknowledge the necessity of this step, one may consult Figure 1 in Davis & Huchra (1982) and Figures 3 and 5 of Choloniewski (1986).] New methods for (M) that do not make the assumption of homogeneity were pioneered by Turner (1979), Kirshner et al. (1979), and A. Yahil (Sandage et al. 1979). The last is a maximum-likelihood method and is discussed below. The basic idea is to consider the ratio of the number of galaxies having absolute magnitudes between M and M + dM to the total number of galaxies brighter than M [in volume dV at a given location (x, y, z)]. Using Equations 8 and 12, we find this ratio to be

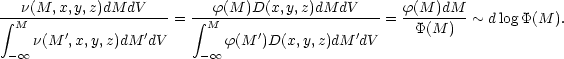
(15)

The main point is that the density function D(x, y, z) cancels out because and D are assumed to be independent. The ratio of the differential to the integrated LF, / (determined in the classical way!), is thus independent of any inhomogeneities in the distribution of galaxies. Integrating / gives log(M), and differentiating (M) back gives (M). A slight variation of the method, by binning the data in equal distance intervals instead of equal magnitude intervals, has been developed and used by Davis et al. (1980) and Davis & Huchra (1982). In principle, no assumption is required about the form of (M), i.e. the / method is nonparametric. However, in practice (M) has always been parametrized. Kirshner et al. (1979) have fitted directly to the corresponding ratio of the Schechter function (cf. Section 3.1, Equation 13). Davis et al. (1980) and Davis & Huchra (1982) made a (form-independent) fourth-order polynomial fit to / , integrated analytically to find , and differentiated back to , which was finally fitted to a Schechter function. A disadvantage of this fitting procedure lies in the large statistical noise of / (see Figure 1 in Kirshner et al. 1979, and Figure 2 in Davis & Huchra 1982).

3.2.3    MAXIMUM-LIKELIHOOD METHODS    Similar to the / method is the method of Sandage et al. (1979), in which a quotient is again considered to make the density function cancel out. Here it is the ratio of the number of galaxies brighter than absolute magnitude M to the total number of galaxies at a given velocity v (i.e. distance). This is simply the probability P(M, v) that a galaxy at v is brighter than M. The LF (M) cannot, however, be directly determined from P(M, v) but has now to be modeled by an analytical expression with parameters to be fixed by a maximum-likelihood technique, namely by maximizing the product L (= likelihood) of the differential probability densities (P / M) taken at all (unbinned) data points (M, v) of the sample. The calculation of P(M, v) also requires knowledge of the sample incompleteness. The explicit correction that Sandage et al. (1979) made for incompleteness (discussed above) can easily be incorporated into the calculation. By maximizing the likelihood product L, the Schechter parameters and M^*, as well as the parameters m_L and m_L of the incompleteness function f (m), were then found simultaneously. A somewhat different completeness function was used earlier by Neyman & Scott (1974), who were among the first to use the maximum-likelihood technique in galaxy statistics.

In contrast to the above method, where the density function D is removed in a rather subtle way, the following methods solve for D and simultaneously. The price, however, is that the spherical symmetry D = D(r) must be assumed, which makes sense only for pencil-beam samples.

A simple maximum-likelihood method to obtain a handle on D is that of Choloniewski (1985), who considers the probability of a galaxy lying in the interval dMdm, which is determined by (M), f (m), and D(µ), with µ being the distance modulus (m - M). D is modeled by a steplike function, by a Schechter function, and the incompleteness f (m) again by a FermiDirac-like equation, whose best-fitting parameters are found as before by maximizing the product of the probability for the individual data points. Yet another maximum-likelihood method is that of Marshall et al. (1983), developed for quasars, and of Choloniewski (1986). The basic feature here is to treat the number of galaxies in the interval dMdz (or of quasars in dMdz) as the result of a random process described by a Poissonian probability distribution, which has (M) and D(r) as ingredients. Marshall et al. (1983) have modeled and D by parametric expressions and determined the most likely values of the parameters in the normal way. Choloniewski (1986), on the other hand, has binned the data in the (M,µ) plane into equal intervals, which leads to steplike functions for and D. In the sense that no specific form of is assumed, his method can be called nonparametric; however, the steps could also be viewed as a set of parameters. A similar, but more general and mathematically more sophisticated, maximum-likelihood method to derive a nonparametric (M) has been developed by Nicoll & Segal (1983).

3.2.4    THE C-METHOD    An assumption-free method to find (M) was own long before it was realized that the classical method should be replaced. This is the so-called C-method of Lynden-Bell (1971), devised and used for quasars (Jackson 1974) and only recently revived and further developed by Choloniewski (1987), who proposed its application to galaxies. The method is simple and elegant. The basic idea is to represent (M) and D(µ) (assuming spherical symmetry) by superpositions of weighted -functions

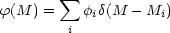
(16)

and

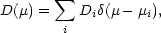
(17)

where i denotes an individual galaxy. The problem is then to determine the coefficients _i and D_i This can be achieved in an almost geometrical way by calculating for every data pointM_i the quantity

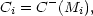
(18)

which is the number of galaxies inside the region

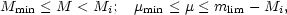
(19)

where M_min and µ_min are appropriate lower limits of M and µ. C^- is called the C-function. If the data points are ordered in such a way that M_{i + 1} M_i, it can be shown that a very simple recursion formula holds for the coefficients _i (see Choloniewski 1987):

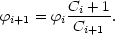
(20)

The analogue holds for the density coefficients D_i. Inserting the resulting _i and D_i into Equations 16 and 17 gives (M) and D(µ), which, however, as weighted sums over -functions have to be smoothed (e.g. by averaging inside appropriate intervals). The revised version by Choloniewski (1987) of this method has yet to be applied to galaxies.

3.2.5    GROUPS    Groups of galaxies comprise at least 70% of all galaxies in the field outside of clusters if galaxies are counted to a faint brightness limit (Holmberg 1969, Tammann & Kraan 1978). Truly "isolated" galaxies are rare (Vettolani et al. 1986). The LF of field galaxies can therefore also be approached by constructing a composite LF of groups of galaxies assuming in first approximation that field and group galaxies have identical LFs. This method is especially valuable for the study of the faint end of the LF because nearby groups (notably the Local Group, and the M81 and M101 groups) have been surveyed to faint flux limits. The LF of an individual group (not the Local Group) follows, like a cluster LF, directly from the distribution of apparent magnitudes and from allowance for the distance modulus of the group. Because the individual groups possess only a few members, their LFs are usually combined into a composite group LF. As with clusters of galaxies, the difficulty lies in the identification of physical group members. Holmberg (1969), who pioneered the method, looked for faint companions close to bright spirals, which he assumed to be at the same distance. After a (very uncertain!) statistical correction for background galaxies (by counting galaxies in nearby comparison fields; see also Section 3.1), he constructed a field LF to a very faint magnitude limit of M ~ -11. Turner & Gott (1976b) derived a composite LF for groups that had been defined by a simple surface density criterion (Turner & Gott 1976a), without any correction for background contamination. The most reliable group LFs are based on nearby groups, where the members can-be identified by morphology and velocity. A useful data base for this task is the catalog of Kraan-Korteweg & Tammann (1979), which lists all galaxies known with v 500 km s^-1. The catalog has been used by Tammann & Kraan (1978), and in a revised version by Tammann (1986), Binggeli (1987), and in the present review (Section 5, Figure 1).

An interesting variation and generalization of the group method, based on the general clustering property of galaxies, has been developed by Yee & Green (1984, 1987) and Phillips & Shanks (1987). The clustering of galaxies, as described by the correlation function (cf. Peebles 1980), means that there is (on average) an excess of galaxies on the sky around any given galaxy, which at small separations must be due to those galaxies that are physically associated with the "center" galaxy and therefore lie at the same distance. Even though it is not known individually which galaxies make up the excess, one can statistically determine the numbers of associated galaxies as a function of magnitude. If the distance of the center galaxy is known, this can be translated into a LF (Yee & Green 1984). By repeating this process for many center galaxies, an LF with good statistical accuracy at the faint end can be obtained (Phillips & Shanks 1987). Yee & Green (1984, 1987) used quasars as center "galaxies" to derive coarse galaxian LFs at high redshifts, but (as previously mentioned) the absolute magnitude calibration depends not only on the value of H₀ adopted but also on q₀ (because the redshifts are large).

Which of the many available methods to determine the LF of field galaxies should best be applied? This is difficult to answer because all post-classical methods (except the group method) have been applied to different samples of galaxies (each chosen by the developers of the method, i.e. there is yet no overlap of different studies applied to the same sample), or else have not been applied to galaxies at all. However, the distinction between parametric or nonparametric LFs is probably not essential. Working parametrically (which applies only to certain maximum-likelihood methods) has the advantage that no data binning is required, but it has the disadvantage that is assumed to have a certain form before the LF is determined. (The goodness of the assumption as to form can of course be tested afterward.) The opposite holds for the nonparametric case, where is represented by a histogram (which, however, in the end is usually fitted to a parametric expression anyway!). The expression adopted by all workers in the field is the Schechter (1976) function (Equation 13), which does model cluster and field LFs quite well (Section 4). The fitting can be done by a simple minimum-² technique, or better (to account for the large errors at the bright and faint ends) by a method that involves the so-called Eddington correction (Trumpler & Weaver 1953, Kiang 1961, Schechter 1976, Felten 1985).

More important is the role of the density function D. Strictly, the / method and the method of Sandage et al. (1979) are the only ones that make no assumption about the form of D. This means that all information about D is lost because D must be determined independently after . All other methods supply D and simultaneously. In the classical method this is the mean density of the Universe, or the "normalization" of , which, as we emphasized earlier, has led to the unfortunate melding together of and D (see Section 2); otherwise it is the density as a function of the distance D = D(r). The price is, of course, that an assumption has to be made about D. We know that D constant, i.e. the classical method is no longer viable. As stated before, methods that assume D = D(r) are ideal for pencil-beam samples, which subtend small solid angles of sky, but for all-sky samples one should rather use the / method or the method of Sandage et al. (1979), which do not assume spherical symmetry.