Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

6.1. Disk Heating by Halo Holes

As halo objects traverse the Galactic disk, they will impart energy to the stars there. This will lead to a gradual puffing up of the disk, with older stars being heated more than younger ones. Lacey & Ostriker (1985) have argued that black holes of around 10⁶ M could provide the best mechanism for generating the observed amount of puffing. In particular, this explains: 1. why the velocity dispersion of the disk stars, , scales with age as t^1/2; 2. the relative velocity dispersions in the radial, azimuthal, and vertical directions; and 3. the existence of a high energy tail of stars with large velocity Ipser & Semenzato 1985). In order to normalize the (t) relationship correctly, the number density of the holes n must satisfy nM² 3 × 10⁴ M² pc^-3. Combining this with the local halo density _h = nM 0.01 M pc^-3 gives M = 2 &215; 10⁶ M.

This argument is no longer compelling because more recent measurements give smaller velocity dispersions for older stars, so that a may no longer rise as fast as t^1/2 (Carlberg et al 1985, Stromgren 1987, Gomez et al 1990). Heating by a combination of spiral density waves and giant molecular clouds may now give a better fit to the data (Lacey 1991). Nevertheless, one can still use the Lacey-Ostriker argument to place an upper limit on the density in halo objects of mass M (Carr et al 1984):

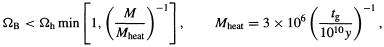
(6.1)

where t_g is the age of the Galaxy. Otherwise the disk would be more puffed up than observed. This limit is shown in Figure 3, along with the line that corresponds to having at least one black hole of mass M within the Galaxy.

Although the dependence is not shown explicitly in Equation (6.1), M_heat also scales as ² and ^-1_h. Thus, by applying the disk-heating argument to galaxies with higher dark matter density, lower stellar velocity dispersion, or smaller age, one can obtain stronger constraints. For the gas-rich dwarf galaxy DDO 154 (which has = 17 km s^-1, an age of at least 1.5 Gyr, and a central dark matter density of 0.009 M pc^-3), Rix & Lake (1993) find M < 7 × 10⁵ M. For the dwarf galaxy GR8 (which has = 4 km s^-1, an age of at least 1 Gyr, and a central dark matter density of 0.07 M pc^-3), they find M < 6 × 10³ M. Of course unless the black holes form pregalactically, there is no reason for expecting the halo objects to have the same mass in different galaxies, so these limits are not shown in Figure 3.