Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

6.2. Disruption of Stellar Clusters by Halo Objects

Another type of dynamical effect associated with halo objects would be their influence on bound groups of stars (in particular, globular clusters and loose clusters). Every time a halo object passes near a star cluster, the object's tidal field heats up the cluster and thereby reduces its binding energy. Over a sufficiently large number of fly-bys this could evaporate the cluster entirely. This process was first discussed by Spitzer (1958) for the case in which the disrupting objects are giant molecular clouds. Carr (1978) used a similar analysis to argue that the halo objects must be smaller than 10⁵ M or else loose clusters would not survive as long as observed - but this argument neglected the fact that sufficiently massive holes will disrupt clusters by single rather than multiple fly-bys. The correct analysis was given by Wielen (1985) for halo objects with the mass of 2 × 10⁶ M required in the Lacey-Ostriker scenario and by Sakellariadou (1984) and Carr & Sakellariadou (1994) for halo objects of general mass. By comparing the expected disruption time for clusters of mass m_c and radius r_c with the typical cluster lifetime t_L, one finds that the local density of halo holes of mass M must satisfy (cf Ostriker et al 1989)

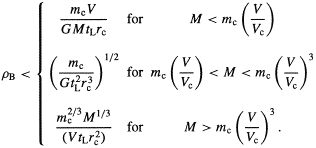
(6.2)

Here V_c ~ (Gm_c / r_c)^1/2 is the velocity dispersion within the cluster, V is the speed of the halo objects (~ 300 km s^-1) and we have neglected numerical factors of order unity. The increasing mass regimes correspond to disruption by multiple encounters, single encounters, and nonimpulsive encounters, respectively. Any lower limit on t_L therefore places an upper limit on _B. The crucial point is that the limit is independent of M in the single-encounter regime, so that the limit bottoms out at a density of order (_c / Gt²_L)^1/2. The constraint is therefore uninteresting if this exceeds the observed halo density _h. In particular, if the clusters survive for the lifetime of the Galaxy, which is essentially the age of the Universe t₀, the limiting density is just (_{c 0})^1/2, where ₀ is the mean cosmological density. If t_L is much larger, than t₀, the fraction of clusters disrupted within t₀ is f_c ~ t₀ / t_L and so the limiting density is reduced by the factor f_c.

The strongest limit is associated with globular clusters, for which we take m_c = 10⁵ M, r_c = 10 pc, V_c = 10 km s^-1, and t_L > 10¹⁰y. We also assume that the holes have a speed V = 300 km s^-1. Rather remarkably, due to the "coincidence" that the halo density is the geometric mean of the cosmological density and the globular cluster density, the upper limit on _B is comparable to the actual halo density; this suggests that halo objects might actually determine the characteristics of surviving globular clusters (cf Fall & Rees 1977). Numerical calculations for the disruption of globular clusters by Moore (1993) confirm the general qualitative features indicated above: gradual mass loss for small halo objects and sudden disruption for larger ones. However, using data for nine particular globular clusters, Moore infers an upper limit of 10³ M. This is in the multiple-encounter regime and considerably stronger than the limit implied by Equation (6.2) with t_L = t₀, presumably because his clusters are very diffuse. Because of the uncertainties, the line corresponding to Moore's result is only shown dotted in Figure 3.