Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

6.4. Is the Halo made of Dark Clusters?

We have seen that both the cluster disruption and dynamical friction constraints may be incompatible with the Lacey & Ostriker proposal that 2 × 10⁶ M halo black holes generate the observed disk-heating. There is also the problem that supermassive halo black holes might generate too much radiation through accretion as they traverse the disk (Ipser & Price 1977). To circumvent these objections, Carr & Lacey (1987) have proposed that the disk heaters are 2 × 10⁶ M clusters of smaller objects rather than single black holes. The accretion luminosity is then reduced by a factor of order the number of objects per cluster and the dynamical friction problem is avoided, provided the clusters are disrupted by collisions before they are dragged into the Galactic nucleus by dynamical friction.

One can extend this idea to a more general cluster scenario (Wasserman & Salpeter 1993, Kerins & Carr 1994, Moore & Silk 1994). If we assume that the clusters all have the same mass M_c and radius R_c, then they will be disrupted by collisions within the Galactocentric radius (6.3) at which dynamical friction operates, providing

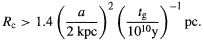
(6.6)

If this condition is not satisfied, then M_c must be less than the value indicated by Equation (6.5). In order to avoid the evaporation of clusters as a result of 2-body relaxation, one also requires

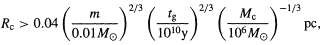
(6.7)

where m is the mass of the components. An upper limit on R_c comes from requiring that the clusters do not disrupt at our own Galactocentric radius R₀ ~ 10 kpc which implies

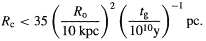
(6.8)

These dynamical limits, together with the disk-heating limit (6.1), are indicated by the bold lines in Figure 4, which show that the values of M_c and R_c are constrained to a rather narrow range. The cluster-disruption upper limit on M_c is not shown because it is rather model-dependent but it could further reduce the range.

Figure 4. Dynamical constraints on the mass Mc and radius Rc of clusters that provide the dark mass in the Galactic halo. Outside the bold lines the clusters are either disrupted by collisions or produce excessive disk heating or evaporate or produce an excessive buildup of mass in the Galactic nucleus as a result of dynamical friction. Also shown are the extended source sensitivity of ISO (for an integration time of 100 s) and IRAS, assuming that the brown dwarfs have the optimal mass of 0.02 M, and the region where the clusters cover the sky.

There is some uncertainty in the positions of the boundaries in Figure 4. If one merely requires that the clusters do not disrupt at the edge of the halo, the upper limit (6.8) is increased by a factor of (R_h / R₀)², as indicated by the dotted line in Figure 4. The dynamical friction limits are sensitive to the value of a: the limits are shown for a = 2 kpc and a = 8 kpc since this spans the range of likely values. The evaporation limit given by Equation (6.7) depends on the value of m: Figure 4 assumes m = 0.02 M. Note that together Equations (6.1), (6.7), and (6.8) require the cluster components to be smaller than 10 M², which probably excludes their being VMO black holes.