Annu. Rev. Astron. Astrophys. 1994. 32: 531-590 Copyright © 1994 by Annual Reviews. All rights reserved

6.3. Effect of Dynamical Friction on Halo Objects

Another important dynamical effect is that halo objects will tend to lose energy to lighter objects and consequently drift toward the Galactic nucleus (Chandrasekhar 1964). In particular, one can show that halo objects will be dragged into the nucleus by the dynamical friction of the Spheroid stars from within a Galactocentric radius

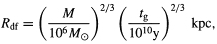
(6.3)

and the total mass dragged into the Galactic nucleus is therefore

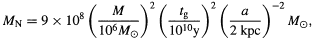
(6.4)

where a is the halo core radius (Carr & Lacey 1987). This exceeds the upper observational limit of 3 × 10⁶ M (Sellgren et al 1990, Spaenhauer et al 1992) unless

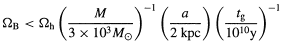
(6.5)

This is certainly stronger than the disk-heating limit; it may also be stronger than the cluster disruption limit.

Although this argument would seem to preclude the Lacey-Ostriker proposal, there is an important caveat in this conclusion (Hut & Rees 1992). Equation (6.4) implies that about 10³ holes of 10⁶ M would have drifted into the Galactic nucleus by now, corresponding to one arrival every 10⁷ y. Once two black holes have reached the nucleus, they will form a binary, which will eventually coalesce due to loss of energy through gravitational radiation. If a third hole arrives before coalescence occurs, then the "slingshot" mechanism could eject one of the holes and the remaining pair might also escape due to the recoil (Saslaw et al 1974). Hut & Rees estimate that the time for binary coalescence is shorter than the interval between infalls, which suggests that the slingshot is ineffective. However, there is another problem with Equation (6.5): Dynamical friction will also deplete the number of stars in the nucleus and this will eventually suppress dynamical friction unless there is an efficient mechanism to replenish the loss-cone (Begelman et al 1980). Limit (6.5) is clearly not completely firm, so it is only shown dotted in Figure 3.