


2.2. The effect on the acoustic peaks
We will now focus our attention on possible effects of primordial magnetic fields on small angular scales. That is, temperature, as well polarization, anisotropies of the CMBR. By small angular scale (< 1°) we mean angles which correspond to a distance smaller than the Hubble horizon radius at the last scattering surface. Therefore, what we are concerning about here are anisotropies that are produced by causal physical mechanisms which are not related to the large scale structure of the space-time.
Primordial density fluctuations, which are necessary to explain the observed structures in the Universe, give rise to acoustic oscillations of the primordial plasma when they enter the horizon some time before the last scattering. The oscillations distort the primordial spectrum of anisotropies by the following primary effects [57]: a) they produce temperature fluctuations in the plasma, b) they induce a velocity Doppler shift of photons, c) they give rise to a gravitational Doppler shift of photons when they climb-out or fall-in the gravitational potential well produced by the density fluctuations (Sachs-Wolfe effect).
In the linear regime, acoustic plasma oscillations are well described by standard fluid-dynamics (continuity + Euler equations) and Newtonian gravity (Poisson's equation). In the presence of a magnetic field the nature of plasma oscillations can be radically modified as Magneto-Hydro-Dynamics (MHD) has to be taken into account.
To be pedagogical, we will first consider a single component plasma and neglect any dissipative effect, due for example to a finite viscosity and heat conductivity. We will also assume that the magnetic field is homogeneous on scales larger than the plasma oscillations wavelength. This choice allows us to treat the background magnetic field B0 as a uniform field in our equations (in the following symbols with the 0 subscript stand for background quantities whereas the subscript 1 is used for perturbations). Within these assumptions the linearized equations of MHD in comoving coordinates are [58] (4)
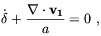
| (2.11) |
where a is the scale factor.
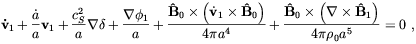
| (2.12) |
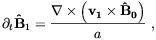
| (2.13) |
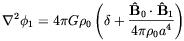
| (2.14) |
and
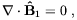
| (2.15) |
where [^(B)]  B a2 and
B a2 and
 =
=
 1
/
1
/  0,
0,
 1 and
v1 are small perturbations
on the background density, gravitational potential and velocity
respectively. cS is the sound velocity.
Neglecting its direct gravitational influence, the magnetic field
couples to fluid dynamics only through the last two terms in
Eq. (12).
The first of these terms is due to the displacement current
contribution to
1 and
v1 are small perturbations
on the background density, gravitational potential and velocity
respectively. cS is the sound velocity.
Neglecting its direct gravitational influence, the magnetic field
couples to fluid dynamics only through the last two terms in
Eq. (12).
The first of these terms is due to the displacement current
contribution to  ×
B, whereas the latter
account for the magnetic force of the current density.
The displacement current term can be neglected provided that
×
B, whereas the latter
account for the magnetic force of the current density.
The displacement current term can be neglected provided that
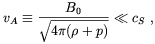
| (2.16) |
where vA is the, so called, Alfvén velocity.
Let us now discuss the basic properties of the solutions of these equations, ignoring for the moment the expansion of the Universe. In the absence of the magnetic field there are only ordinary sound waves involving density fluctuations and longitudinal velocity fluctuations (i.e. along the wave vector). By breaking the rotational invariance, the presence of a magnetic field allows new kind of solutions that we list below (useful references on this subject are [59, 60]).
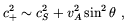
| (2.17) |
where  is the angle
between k and B0.
Fast magnetosonic waves involve fluctuations in the velocity,
density, magnetic field and gravitational field. The velocity
and density fluctuations are out-of-phase by
is the angle
between k and B0.
Fast magnetosonic waves involve fluctuations in the velocity,
density, magnetic field and gravitational field. The velocity
and density fluctuations are out-of-phase by
 / 2.
Eq. (2.17) is valid for
vA << cS. For such fields
the wave is approximatively longitudinal.
/ 2.
Eq. (2.17) is valid for
vA << cS. For such fields
the wave is approximatively longitudinal.
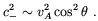
| (2.18) |
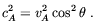
| (2.19) |
Detailed treatments of the evolution of MHD modes in the matter dominated and radiation dominated eras of the Universe can be found in Refs. [61, 62].
The possible effects of MHD waves on the temperature anisotropies of the CMBR has been first investigated by Adams et al. [58] In the simplest case of magnetosonic waves, they found that the linearized equations of fluctuations in the Fourier space are
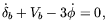
| (2.20) |
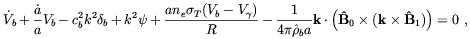
| (2.21) |
for the baryon component of the plasma and
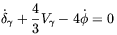
| (2.22) |

| (2.23) |
for the photon component.
In the above V = i k · v, R =
(pb +
 b) /
(p
b) /
(p +
+ 
 )
= (3
)
= (3  b) /
(4
b) /
(4
 ) and
cb is the baryon sound velocity in the absence
of interactions with the photon gas.
As it is evident from the previous equations, the coupling between the
baryon and the photons fluids is supplied by Thomson scattering
with cross section
) and
cb is the baryon sound velocity in the absence
of interactions with the photon gas.
As it is evident from the previous equations, the coupling between the
baryon and the photons fluids is supplied by Thomson scattering
with cross section
 T.
T.
In the tight coupling limit (Vb ~
V )
the photons provide the baryon fluid with a pressure term and a
non-zero sound velocity.
The magnetic field, through the last term in Eq. (1.21),
gives rise to an additional contribution to the effective
baryon sound velocity. In the case of longitudinal waves this
amounts to the change
)
the photons provide the baryon fluid with a pressure term and a
non-zero sound velocity.
The magnetic field, through the last term in Eq. (1.21),
gives rise to an additional contribution to the effective
baryon sound velocity. In the case of longitudinal waves this
amounts to the change
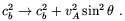
| (2.24) |
In other words, the effect of the field can be somewhat mimicked by a variation of the baryon density. A complication arises due to the fact that the velocity of the fast waves depends on the angle between the wave-vector and the magnetic field. As we mentioned previously, we are assuming that the magnetic field direction changes on scales larger than the scale of the fluctuation. Different patches of the sky might therefore show different fluctuation spectra depending on this angle.
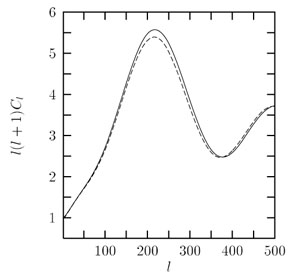
|
Figure 2.1. The effect of a cosmic magnetic
field on the multipole
moments. The solid line shows the prediction of a standard CDM cosmology
( |
The authors of Ref.
[58]
performed an all-sky average
summing also over the angle between the field and the
line-of-sight. The effect on the CMBR temperature power spectrum
was determined by a straightforward modification of the CMBFAST
[63]
numerical code. From the Fig. 2.1 the reader can
see the effect of a field B0 = 2 ×
10-7 G on the first
acoustic peak. The amplitude of the peak is reduced with respect
to the free field case. This is a consequence of the magnetic
pressure which opposes the in-fall of the photon-baryon fluid in
the potential well of the fluctuation. Although this is not
clearly visible from the figure, the variation of the sound
velocity, hence of the sound horizon, should also produce a
displacement of the acoustic peaks. The combination of these two
effects may help to disentangle the signature of the magnetic field from
other cosmological effects (for a comprehensive review see
[64])
once more precise observations of the CMBR power
spectrum will be available. Adams at al. derived an estimate of the
sensitivity to B which MAP
[66]
and PLANCK [67]
satellites observations
should allow to reach by translating the predicted sensitivity of these
observations to
 b. They
found that a magnetic field with strength today
B0 > 5 × 10-8 G should be detectable.
b. They
found that a magnetic field with strength today
B0 > 5 × 10-8 G should be detectable.
It is interesting to observe that a magnetic field cannot lower the ratio of the first to second acoustic peak as showed by recent observations [65].
Alfvén waves may also leave a signature on the CMBR anisotropies. There are at least three main reasons which make this kind of wave of considerable interest. The first is that Alfvén waves should leave a quite peculiar imprint on the CMBR power spectrum. In fact, as we discussed in the above, these waves do not involve fluctuations in the density of the photon-baryon fluid. Rather, they consist only of oscillations of the fluid velocity and of the magnetic field. Indeed, by assuming that the wavelength is smaller than the Hubble radius and that relativistic effects are negligible, the equations describing Alfvén waves are [58]
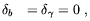
| (2.25) |

| (2.26) |
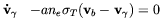
| (2.27) |
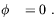
| (2.28) |
Since the gravitational Doppler shift (Sachs-Wolfe effect) is absent in this case, the cancellation against the velocity Doppler shift which occurs for the acoustic modes [57] does not take place for the Alfvén waves. This could provide a more clear signature of the presence of magnetic fields at the last scattering surface [58].
The second reason why Alfvén waves are so interesting in this
contest is that they are vector (or rotational) perturbations.
As a consequence they are well suited to probe peculiar initial condition
such as those that might be generated from primordial phase-transitions.
It is remarkable that whereas vector perturbations are suppressed
by universe expansion and cannot arise from small deviations from the
isotropic Friedmann Universe for t
 0
[53],
this is not true in the presence of a cosmic magnetic field
(5)
0
[53],
this is not true in the presence of a cosmic magnetic field
(5)
The third reason of our interest for Alfvèn waves is that for this kind of waves the effect of dissipation is less serious than what it is for sound and fast magnetosonic waves. This issue will be touched upon in the next section.
A detailed study of the possible effects of Alfvén waves on the CMBR anisotropies has been independently performed by Subramanian and Barrow [69] and Durrer at al. [70] who reached similar results. We summarize here the main points of the derivation as given in Ref. [70].
In general, vector perturbations of the metric have the form
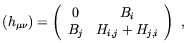
| (2.29) |
where B and H are divergence-free, 3d vector fields supposed to vanish at infinity. Two gauge-invariant quantities [71] are conveniently introduced by the authors of Ref. [70]:
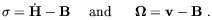
| (2.30) |
which represents the vector contribution to the perturbation of the extrinsic curvature and the vorticity. In the absence of the magnetic field, and assuming a perfect fluid equation of state, the vorticity equation of motion is
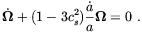
| (2.31) |
In the radiation dominated era the solution of this equation is
 = const. which
clearly does not describe waves and,
as we mentioned, is incompatible with an isotropic universe when
t
= const. which
clearly does not describe waves and,
as we mentioned, is incompatible with an isotropic universe when
t  0. In the
presence of the magnetic field, Durrer et al. found
0. In the
presence of the magnetic field, Durrer et al. found
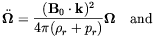
| (2.32) |

| (2.33) |
These equations describe Alfvén waves propagating at the velocity
vA(e ·
(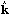 )), where
vA is the Alfvén velocity
and e is the unit vector in the direction of the magnetic
field (6)
In this case some amount of initial vorticity is allowed which is
connected to the amplitude of the magnetic field perturbation
B1
)), where
vA is the Alfvén velocity
and e is the unit vector in the direction of the magnetic
field (6)
In this case some amount of initial vorticity is allowed which is
connected to the amplitude of the magnetic field perturbation
B1
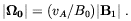
| (2.34) |
The general form of the CMBR temperature anisotropy produced by vector perturbations is

| (2.35) |
where V =  -
-  is a gauge-invariant
generalization
of the velocity field. We see from the previous equation that besides the
Doppler effect Alfvèn waves gives rise to an integrated Sachs-Wolfe
term. However, since the geometric perturbation
is a gauge-invariant
generalization
of the velocity field. We see from the previous equation that besides the
Doppler effect Alfvèn waves gives rise to an integrated Sachs-Wolfe
term. However, since the geometric perturbation
 is decaying
with time, the integrated term is dominated by its lower boundary and just
cancels
is decaying
with time, the integrated term is dominated by its lower boundary and just
cancels  in V.
Neglecting a possible dipole contribution from vector perturbations
today, Durrer at al. obtained
in V.
Neglecting a possible dipole contribution from vector perturbations
today, Durrer at al. obtained
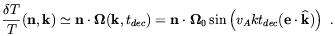
| (2.36) |
As predicted in Ref. [58], Alfvén waves produce Doppler peaks with a periodicity which is determined by the Alfvén velocity. Since, for reasonable values of the magnetic field strength, vA << 1 this peaks will be quite difficult to detect.
Durrer et al. argued that Alfvén waves may leave a
phenomenologically more
interesting signature on the statistical properties of the CMBR
anisotropies.
In the absence of the magnetic field all the relevant information is
encoded in the
C 's
coefficients defined by
's
coefficients defined by
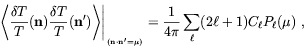
| (2.37) |
where µ  n · n'. By introducing the usual
spherical harmonics decomposition
n · n'. By introducing the usual
spherical harmonics decomposition
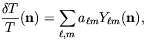
| (2.38) |
the C 's
are just
's
are just
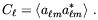
| (2.39) |
Because of its spin-1 nature, the vorticity vector field induces
transitions 

 ± 1 hence a
correlation between the multipole amplitudes
a
± 1 hence a
correlation between the multipole amplitudes
a +1, m and
a
+1, m and
a -1, m.
This new kind of correlation is encoded in the coefficients
-1, m.
This new kind of correlation is encoded in the coefficients
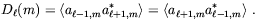
| (2.40) |
Durrer at al. [70]
determined the form of the
C and
D
and
D coefficients for the case of a homogeneous background magnetic field
in the range -7 < n < - 1, where n determine the
vorticity power spectrum according to
coefficients for the case of a homogeneous background magnetic field
in the range -7 < n < - 1, where n determine the
vorticity power spectrum according to
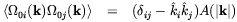
| (2.41) |
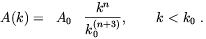
| (2.42) |
On the basis of these considerations they found that 4-year COBE data allow to obtain a limit on the magnetic field amplitude in the range -7 < n < - 3 on the order of (2-7) × 10-9 Gauss.
4 Similar equations were derived by Wasserman [25] to the purpose to study the possible effect of primordial magnetic fields on galaxy formation. Back.
5 Collisionless matter, like e.g. gravitons after the Planck era, may however support nonzero vorticity even with initial conditions compatible with an isotropic universe [68]. Back.
6 Differently form the authors of Ref. [58], Durrer at al. assumed a homogeneous background magnetic field. This however is not a necessary condition for the validity of the present considerations. Back.