2.3. Dissipative effects on the MHD modes

In the previous section we neglected any dissipative effect which may possibly affect the evolution of the MHD modes. However, similar to the damping of baryon-photon sound waves by photon shear viscosity and heat conductivity, damping of MHD perturbations may also occur. This issue was studied in detail by Jedamzik, Katalinic and Olinto [72] who first determined the damping rates of fast and slow magnetosonic waves as well as of Alfvén waves. Furthermore, it was shown in Refs. [72, 73] that dissipation of MHD modes produce an effective damping of inhomogeneous magnetic fields. The dissipation process goes as follows. A spatially tangled magnetic field produces Lorentz forces which accelerate the plasma and set up oscillations. Since the radiation-baryon pressure is much larger than the magnetic pressure, as long as the photon mean-free-path is smaller than the scale of the magnetic tangle, the motions can be considered as being largely incompressible. In this situation mainly Alfvén waves, which do not involve density fluctuations, are excited. In the absence of dissipation, this process will continue until, for all scales with magnetic field relaxation time ~ / v_A shorter than the Hubble time t_H, an approximate equipartition between magnetic and kinetic energies is produced. If the fluid is non-ideal, however, shear viscosity will induce dissipation of kinetic energy, hence also of magnetic energy, into heat. In this case dissipation will end only when the magnetic field reaches a force-free state.

In the absence of magnetic fields it is known that in the diffusive regime (i.e. when the perturbation wavelength is much larger than the mean free path of photon or neutrinos) acoustic density fluctuations are effectively damped because of the finite viscosity and heat conductivity (Silk damping [74]). At recombination time, dissipation occurs for modes smaller than the approximate photon diffusion length, d ~ (l t_H)^1/2, where l is photon mean free path. The dissipation of fast magnetosonic waves proceeds in a quite similar way. Indeed, it was showed in Ref. [72] that the dissipation length scale of these kind of waves coincide with the Silk damping scale. More interesting is the result found in Refs. [72, 73] which shows that damping of Alfvén and slow magnetosonic waves is significantly different from damping of sound and fast magnetosonic waves. The reason for such a different behavior is that, for a small background magnetic field v_A << 1 so that the oscillation frequency of an Alfvén mode (v_A k / a) is much smaller than the oscillation frequency of a fast magnetosonic mode with the same wavelength (v_sound k / a). While all magnetosonic modes of interest satisfy the condition for damping in the oscillatory regime (v_sound << l k / a), an Alfvén mode can become overdamped when the photon (or neutrino) mean-free-path becomes large enough for dissipative effects to overcome the oscillations (v_A cos l(T) k / a, where is the angle between the background magnetic field and the wave vector). Because of the strong viscosity, that prevent fluid acceleration by the magnetic forces, damping is quite inefficient for non-oscillating overdamped Alfvén modes with

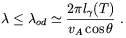
(2.43)

As a result, the damping scale of overdamped Alfvén modes at the end of the diffusion regime is smaller than the damping scale of sound and fast magnetosonic modes (Silk damping scale) by a factor which depends on the strength of the background magnetic field and the angle, L_A ~ v_A cos d.

From the previous considerations it follows that the results discussed in the previous section hold only under the assumption that the magnetic field coherence length is not much smaller than the comoving Silk damping scale (L_S ~ 10 Mpc), in the case of fast magnetosonic waves, and not smaller than L_A for Alfvén waves.

Some other interesting work has been recently done by Jedamzik, Katalinic and Olinto [75] concerning the effects of dissipation of small-scale magnetic fields on the CMBR. The main idea developed in the paper by Jedamzik et al. is that the dissipation of tangled magnetic fields before the recombination epoch should give rise to a nonthermal injection of energy into the heat-bath which may distort the thermal spectrum of CMBR. It was showed by the authors of Ref. [75] that once photon equilibration has occurred, mainly via photon-electron scattering and double-Compton scattering, the resultant distribution should be of Bose-Einstein type with a non-vanishing chemical potential. The evolution of the chemical potential distortions at large frequencies may be well approximated by [76]

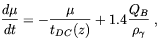
(2.44)

where, in our case, Q_B = d_B / dt is the dissipation rate of the magnetic field and t_DC = 2.06 × 10³³ s (_b h²)^-1 z^-9/2 is a characteristic time scale for double-Compton scattering. Jedamzik et al. assumed a statistically isotropic magnetic field configuration with the following power spectrum

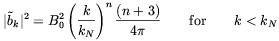
(2.45)

and zero otherwise, normalized such that <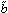²> = B₀². The energy dissipation rate was determined by substituting this spectrum in the following Fourier integral

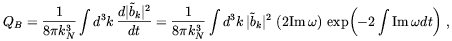
(2.46)

together with the mode frequencies for Alfvén and slow magnetosonic waves determined in Ref. ([72])

(2.47)

where 3( + p)' = , and is the shear viscosity. For k_N >> k_D⁰ z_µ^3/2, where k_D⁰ = (15n_e⁰ _Th / 2.39 × 10¹9 s)^1/2, an analytic solution of Eq. (2.44) was then found to be

(2.48)

In the above K is a numerical factor of order 1, the precise value depending on the spectral index n and z_µ is the characteristic redshift for "freze-out" from double-Compton scattering. This redshift equals z_µ = 2.5 × 10⁶ for typical values _b h² = 0.0125, and Y_p = 0.24. The scale k_D⁰ z_µ^3/2 has a simple interpretation. It is the scale which at redshift z_µ is damped by one e-fold. For the above values of _b h² and Y_p the corresponding comoving wavelength is _D = (2) / (k_D⁰ z_µ^3/2) = 395 pc.

The present upper limit on chemical potential distortion of the CMBR come from the COBE/FIRAS data: |µ| < 9 × 10^-5 at 95% confidence level [77]. Comparing this limit with the prediction of Eq. (2.48) it follows that primordial magnetic fields of strength 3 × 10^-8 G, and comoving coherence length 400 pc are probably excluded. On slightly larger scales, dissipation of spatially tangled magnetic fields may give to a different kind of CMBR distortion which may be described by a superposition of blackbodies of different temperature, i.e. a Compton y distortion [78]. The absence of this kind of distortions in the observed CMBR thermal spectrum disallow magnetic fields of 3 × 10^-8 Gauss on scales ~ 0.6 Mpc.