


2.4. Effects on the CMBR polarization
Thomson scattering is a natural polarizing mechanism for the CMBR. It is enough if the photon distribution function seen by the electrons has a quadrupole anisotropy to obtain polarization. At early times, the tight coupling between the photons and the electron-baryon fluid prevents the development of any photon anisotropy in the baryon's rest frame, hence the polarization vanishes. As decoupling proceeds, the photons begin to free-stream and temperature quadrupole anisotropies can source a space dependent polarization. For this reason temperature and polarization anisotropies are expected to be correlated (for a comprehensive review on the subject see [79]).
The expected polarization anisotropy is not large, perhaps about 10-6. Currently the best polarization limit comes from the Saskatoon experiment [80], with a 95% confidence level upper limit of 25 µK at angular scales of about a degree, corresponding to 9 × 10-6 of the mean temperature. Future balloons and satellites observations, like e.g. the PLANCK [67] mission to be launched in 2007, are expected to have a good chance to measure the CMBR polarization power spectrum.
Kosowsky and Loeb [81] first observed that the possible presence of magnetic fields at the decoupling time may induce a sizeable Faraday rotation in the CMBR. Since the rotation angle depend on the wavelength, it is possible to estimate this effect by comparing the polarization vector on a given direction at two different frequencies. The basic formula is [15]
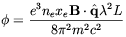
| (2.49) |
where  is the amount by
which the plane of polarization of linearly
polarized radiation has been rotated, after traversing a distance L in a
homogeneous magnetic field B in a direction
is the amount by
which the plane of polarization of linearly
polarized radiation has been rotated, after traversing a distance L in a
homogeneous magnetic field B in a direction
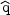 .
xe is the ionized fraction of the total electron
density ne and m is the electron mass. Finally
.
xe is the ionized fraction of the total electron
density ne and m is the electron mass. Finally
 is the radiation
wavelength.
is the radiation
wavelength.
Although the magnetic field strength is expected to be larger at early times, the induced Faraday rotation depends also on the free electron density (see Eq. (2.49)) which drops to negligible values as recombination ends. Therefore, rotation is generated during the brief period of time when the free electron density has dropped enough to end the tight coupling but not so much that Faraday rotation ceases. A detailed computation requires the solution of the radiative transport equations in comoving coordinates [81]
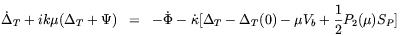
| (2.50) |
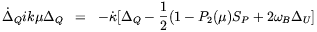
| (2.51) |
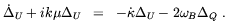
| (2.52) |
In the above
 T,
T,
 Q and
Q and
 U
respectively represent the fluctuations of temperature and of the
of the Stokes parameters Q and U
[15].
The linear polarization is
U
respectively represent the fluctuations of temperature and of the
of the Stokes parameters Q and U
[15].
The linear polarization is
 P
= sqrt[
P
= sqrt[ Q2 +
Q2 +
 U2].
The numerical subscripts on the radiation brightnesses
U2].
The numerical subscripts on the radiation brightnesses
 X
indicate moments defined by an expansion of the
directional dependence in Legendre polynomials
P
X
indicate moments defined by an expansion of the
directional dependence in Legendre polynomials
P (µ):
(µ):
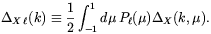
| (2.53) |
Therefore, the subscripts 0, 1, 2 label respectively monopole, dipole and
quadrupole moments.
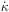 =
xe ne
=
xe ne
 T
T
 / a
is the differential optical depth and the quantities Vb and R
have been defined in the previous section.
Derivatives are respect to conformal time.
Finally,
/ a
is the differential optical depth and the quantities Vb and R
have been defined in the previous section.
Derivatives are respect to conformal time.
Finally,  B is
the Faraday rotation rate
B is
the Faraday rotation rate
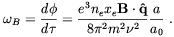
| (2.54) |
From Eqs. (2.51, 2.52) wee see that Faraday rotation mixes Q
and U Stokes parameters. The polarization brightness
 Q is induced
by the function SP =
-
Q is induced
by the function SP =
- T(2)
-
T(2)
-  Q(2)
+
Q(2)
+  Q(0)
and
Q(0)
and  U is
generated as
U is
generated as
 Q and
Q and
 U are
rotated into each other. In the absence of magnetic
fields,
U are
rotated into each other. In the absence of magnetic
fields,  U
retains its tight-coupling value of zero.
The set of Eqs. (2.50-2.52) is not easily solved. A convenient
approximation is the tight coupling approximation which is an expansion
in powers of k
U
retains its tight-coupling value of zero.
The set of Eqs. (2.50-2.52) is not easily solved. A convenient
approximation is the tight coupling approximation which is an expansion
in powers of k
 C with
C with
 C =
C =
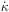 -1.
This parameter measures the average conformal time between collisions.
At decoupling the photon mean free
path grows rapidly and the approximation breaksdown, except for long
wavelength as measured with respect to the thickness of the last scattering
surface. For these frequencies the approximation is still accurate.
-1.
This parameter measures the average conformal time between collisions.
At decoupling the photon mean free
path grows rapidly and the approximation breaksdown, except for long
wavelength as measured with respect to the thickness of the last scattering
surface. For these frequencies the approximation is still accurate.
Kosowsky and Loeb assumed a uniform magnetic field on the scale of the
width of the last scattering surface, a comoving scale of about 5 Mpc. This
assumption is natural if the coherent magnetic field observed in galaxies
comes from a primordial origin, since galaxies were assembled from a
comoving
scale of a few Mpc. The mean results was obtained by averaging over the
entire sky. Therefore the equations still depend only on k and
µ = cos(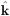 ·
· 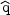 )
and not on the line-of-sight vector
)
and not on the line-of-sight vector
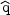 and the
perturbation wave-vector k separately.
The evolution of the polarization brightnesses, for given values of
k and µ is represented in
Fig. 2.2 as a function of the redshift.
and the
perturbation wave-vector k separately.
The evolution of the polarization brightnesses, for given values of
k and µ is represented in
Fig. 2.2 as a function of the redshift.
By following the approach described in the above Kosowsky and Loeb
estimated the polarization angle produced by a magnetic field on CMB
photons with frequency
 1 <
1 <
 2 to be
2 to be
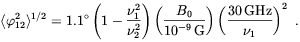
| (2.55) |
A 10% correction may apply to this expression to account for the effects
 b
h2 and
b
h2 and
 0
h2 (in the range
0
h2 (in the range
 b
h2 > 0.007
and
b
h2 > 0.007
and  0
h2 < 0.3).
0
h2 < 0.3).
For a primordial field of B0 ~ 10-9 G which could result in the observed galactic field without dynamo amplification, one can therefore expect a rotation measure of order 1.6 deg cm-2 = 280 rad m-2. This rotation is considerable by astrophysical standards and could in principle be measured.
We noticed at the beginning of this section that temperature and
polarization
anisotropies of the CMBR are generally expected to be correlated. The
statistical properties of such correlation may be affected by the presence
of a magnetic field at the decoupling time in a peculiar way. In fact,
it was showed by Scannapieco and Ferreira
[82] that
such a field may induce an observable parity odd cross correlation between
polarization and temperature anisotropies.
Any polarization pattern on the sky can be separated into "electric"
(E) and "magnetic" (B) components. The nomenclature
reflects the global parity
property. Like multipole radiation, the harmonics of an E-mode have
(-1) parity on
the sphere, whereas those of a B-mode have
(-1)
parity on
the sphere, whereas those of a B-mode have
(-1) +1 parity.
Indeed, given a measurement of the Stokes parameters Q and
U, this data can be decomposed into a sum over spin ± 2
spherical harmonics
+1 parity.
Indeed, given a measurement of the Stokes parameters Q and
U, this data can be decomposed into a sum over spin ± 2
spherical harmonics
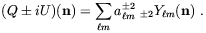
| (2.56) |
Under parity inversion,
sY m
m
 (-1)
(-1) sY
sY m
so that
2Y
m
so that
2Y m
±
-2Y
m
±
-2Y m
are parity eigenstates.
It is then convenient to define the coefficients
m
are parity eigenstates.
It is then convenient to define the coefficients
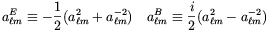
| (2.57) |
so that the E-mode remains unchanged under parity inversion
for even  , whereas the
B-mode changes sign.
, whereas the
B-mode changes sign.
In an isotropic Universe, cross correlation between the B and E polarizations is forbidden as this would imply parity violation. Magnetic fields, however, are maximally parity violating and therefore they may reveal their presence by producing such a cross correlation, Faraday rotation being the physical process which is responsible for this effect. The authors of Ref. [82] determined the expected cross correlation between temperature and E and B polarization modes. On the basis of such result they concluded that magnetic fields strengths as low as 10-9 (present time value obtained assuming adiabatic scaling) could be detectable by the PLANCK satellite mission. It is worthwhile to note that Scannapieco and Ferreira only considered homogeneous magnetic fields. We note, however, that most of their considerations should apply also to the case of magnetic fields with a finite coherence length. In this case measurements taken in different patches of the sky should present different temperature-polarization cross correlation depending on the magnetic field and the line-of-sight direction angle.
The consequences of Faraday rotation may go beyond the effect they produce on the CMBR polarization. Indeed, Harari, Hayward and Zaldarriaga [83] observed that Faraday rotation may also perturb the temperature power spectrum of CMBR. The effect mainly comes as a back-reaction of the radiation depolarization which induces a larger photon diffusion length reducing the viscous damping of temperature anisotropies.
In the absence of the magnetic field
( B = 0), to
the first order in the tight-coupling approximation one finds
B = 0), to
the first order in the tight-coupling approximation one finds
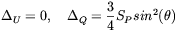
| (2.58) |
and
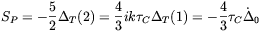
| (2.59) |
 0 =
0 =
 T(0)
+
T(0)
+  . Obviously, all
multipoles with l > 3 vanish to this order. Replacing all
quantities in terms of
. Obviously, all
multipoles with l > 3 vanish to this order. Replacing all
quantities in terms of
 0 one
obtains [84]:
0 one
obtains [84]:
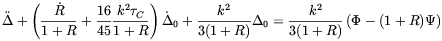
| (2.60) |
that can be interpreted as the equation of a forced oscillator in the presence of damping.
In the presence of the magnetic field
 B
B
 0.
The depolarization depends upon two angles: a) the angle between the
magnetic field and wave propagation and b) the angle of the field with the
wave vector k. Since we assume that the vector k is
determined by stochastic Gaussian fluctuations, its spectrum will have no
preferred direction.
Therefore this dependence will average out when integrated.
It is also assumed that for evolution purposes, the magnetic field has no
component perpendicular to k.
This imposed axial symmetry is compatible with the derivation of the above
written Boltzmann equations. Under these assumptions Harari et al. found
[83]
0.
The depolarization depends upon two angles: a) the angle between the
magnetic field and wave propagation and b) the angle of the field with the
wave vector k. Since we assume that the vector k is
determined by stochastic Gaussian fluctuations, its spectrum will have no
preferred direction.
Therefore this dependence will average out when integrated.
It is also assumed that for evolution purposes, the magnetic field has no
component perpendicular to k.
This imposed axial symmetry is compatible with the derivation of the above
written Boltzmann equations. Under these assumptions Harari et al. found
[83]
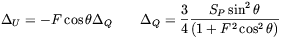
| (2.61) |
where the coefficient F was defined by

| (2.62) |
which gives
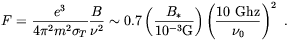
| (2.63) |
Physically, F represents the average Faraday rotation between two photon-electron scattering. Note that assuming perfect conductivity

| (2.64) |
and therefore F is a time independent quantity.
Faraday rotation between collisions becomes considerably large at
frequencies around and below
 d. This quantity is
implicitly defined by
d. This quantity is
implicitly defined by
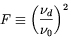
| (2.65) |
which gives
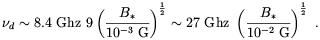
| (2.66) |
From Eqs. (2.61) and, the definition of SP given in the first part of this section, one can extract
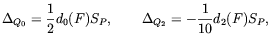
| (2.67) |
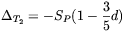
| (2.68) |
and, from the equation for
 T in the
tight coupling,
T in the
tight coupling,
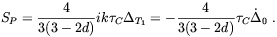
| (2.69) |
In the above the coefficients are defined so that di
 1 +
O(F2) for small F, i.e. small Faraday
rotation, while di
1 +
O(F2) for small F, i.e. small Faraday
rotation, while di
 O(1 /
F)
as F
O(1 /
F)
as F 
 (for the exact
definition see Ref.
[83]).
Equations (2.61, 2.68) and (2.69) condense the main effects of
a magnetic field upon polarization.
When there is no magnetic field (F = 0, d = 1)
(for the exact
definition see Ref.
[83]).
Equations (2.61, 2.68) and (2.69) condense the main effects of
a magnetic field upon polarization.
When there is no magnetic field (F = 0, d = 1)
 U = 0 and
U = 0 and
 Q =
-15/8
Q =
-15/8
 T2
sin2
T2
sin2  . A
magnetic field generates
. A
magnetic field generates
 U,
through Faraday rotation, and reduces
U,
through Faraday rotation, and reduces
 Q. In the
limit of very large F
(large Faraday rotation between collisions) the polarization vanishes.
The quadrupole anisotropy
Q. In the
limit of very large F
(large Faraday rotation between collisions) the polarization vanishes.
The quadrupole anisotropy
 T2
is also reduced by the depolarizing effect of the
magnetic field, by a factor 5/6 in the large F limit, because
of the feedback of
T2
is also reduced by the depolarizing effect of the
magnetic field, by a factor 5/6 in the large F limit, because
of the feedback of
 Q upon
the anisotropy or, in other words, because of the polarization dependence of
Thomson scattering. The dipole
Q upon
the anisotropy or, in other words, because of the polarization dependence of
Thomson scattering. The dipole
 T1
and monopole
T1
and monopole
 T0
are affected by the magnetic field only
through its incidence upon the damping mechanism due to photon
diffusion for small wavelengths. Indeed, the equation for
T0
are affected by the magnetic field only
through its incidence upon the damping mechanism due to photon
diffusion for small wavelengths. Indeed, the equation for
 0
=
0
=  T0
+
T0
+  ,
neglecting O(R2) contributions, now reads
,
neglecting O(R2) contributions, now reads
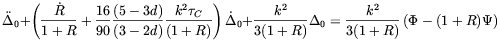
| (2.70) |
which is the equation of a damped harmonic oscillator.
The damping of the temperature anisotropies on small angular scales can be determined by solving the radiative transfer equation to second order in the tight-coupling approximation. By assuming solutions of the form
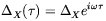
| (2.71) |
for X = T, Q, and U, and similarly for the baryon velocity Vb, Harari et al. [83] found the following solution for Eq. (2.70)
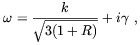
| (2.72) |
where the photon-diffusion damping length-scale is
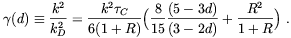
| (2.73) |
The damping affects the multipole coefficients of the anisotropy power spectrum which are defined by
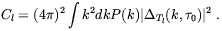
| (2.74) |
The average damping factor due to photon diffusion upon the
Cl's is given by an integral of
e-2 times the visibility function across the last scattering surface
[84,
85].
It depends upon cosmological parameters, notably R, and upon the
recombination history.
times the visibility function across the last scattering surface
[84,
85].
It depends upon cosmological parameters, notably R, and upon the
recombination history.
In the Fig. 2.3 it is represented the
correction to the temperature power spectrum expected for several values
of the parameter F.
We see from that figure that on small angular scales the effect of the
magnetic field
is to increase the temperature anisotropies. The magnitude of this
effect was estimated to be up to 7.5% in a CDM Universe
on small angular scales (l
 1000) at a level that
should be reachable from future CMBR satellite experiments like MAP
[66]
and PLANCK [67].
The frequency at which the effect should be detectable will, however,
depend on the strength and coherence length of the magnetic field at the
recombination time. Both experiment should be sensitive to magnetic fields
around Bz = 1000 = 0.1 G or, equivalently,
B0 =
10-7 G a level that is comparable to be BBN limit (see
Chap. 3).
1000) at a level that
should be reachable from future CMBR satellite experiments like MAP
[66]
and PLANCK [67].
The frequency at which the effect should be detectable will, however,
depend on the strength and coherence length of the magnetic field at the
recombination time. Both experiment should be sensitive to magnetic fields
around Bz = 1000 = 0.1 G or, equivalently,
B0 =
10-7 G a level that is comparable to be BBN limit (see
Chap. 3).