The study of the influence of magnetic fields on the Big Bang Nucleosynthesis (BBN) began with the pioneering works of Matese and O'Connell [86, 87, 88] and Greenstein [89]. It is remarkable that most of the more relevant effects were already pointed-out in those early papers.
In their first paper on the subject Matese and O'Connell
[86]
showed that in the presence of very strong
magnetic fields, B > Bc
eB /
me2 = 4.4 × 1013 G
(above this field strength quantized magnetic levels, "cyclotron
lines", appear), the
decay rate
of neutrons is significantly increased. This is mainly a consequence of the
periodicity of the electron wave function in the plane normal to
the field which turns into an enlarging of the electron available
phase-space. Since the magnetic fields required to obtain any sizeable
effect
cannot be reached in the laboratory in the foreseeable future, Matese
and O'Connell addressed their attention to the early Universe. The
effects of primordial magnetic fields on the production of
4He during BBN was first considered in Ref.
[87]. On the basis of the
results obtained in their previous work
[86], Matese
and O'Connell argued that strong magnetic fields should suppress the
4He
relic abundance with respect to the standard case. Briefly, their
argument was the following. Since, after the neutron to proton
ratio has been frozen, it takes some time for neutrons to be
bounded into composite nuclei, a faster neutron decay due to the
magnetic field implies smaller relic abundances of 4He and of
the heavier elements.
In Ref. [87] two other possible effects of a magnetic field on BBN were shortly considered. The first of these effects consists in the variation that a strong magnetic field induces on the energy density of the electron-positron gas. This effect is a consequence of the grow of the electron and positron phase-space in the presence of over-critical (B > Bc) magnetic fields. Below we shall show how such an effect may have relevant consequences on the BBN through its action on the expansion rate of the Universe and the entropy transfer from the e+ e- gas to the photons. The second effect touched by Matese and O'Connell concerns the influence of a uniform magnetic field on the Universe geometry and its consequences on the BBN (7). Matese and O'Connell analysis of these two effects was only qualitative and, as far as we know, no further work was published by these authors about these issues.
In spite of the large number of effects considered in Ref. [87] Matese and O'Connell did not include in their analysis a simpler and quantitatively more relevant effect of magnetic fields on the BBN, namely the direct contribution of the magnetic field energy density to the expansion rate of the Universe. The relevance of such effect was realized by Greenstein [89] shortly after the publication of the Matese and O'Connell paper. Greenstein showed that by increasing the Universe expansion rate the presence of the magnetic field also increases the temperature at which the neutron-proton equilibrium ratio is frozen. Since this ratio is roughly given by [46]
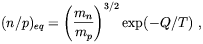
| (3.1) |
where Q
mn - mp, a small
change in the
freezing temperature gives rise to a large variation in the
neutron relative abundance hence in the relic abundance of
the light elements. In his paper Greenstein also noted that if the
magnetic field is
sufficiently tangled over distances small compared to the events
horizon, it will have no effect on the Universe geometry. An
explicit calculations of the 4He relic abundance as a function
of the magnetic field strength were reported in a previous paper by the same
author [90].
Greenstein concluded that the effect
of the magnetic field energy density overcomes that of the magnetic
field on the neutron
decay discussed by Matese and O'Connell. Furthermore, from the
requirement that the relic 4He mass fraction does not exceed
the 28%, he inferred the upper limit B
1012
Gauss at
the time when T = 5 × 109 °K.
In a following paper by Matese and O'Connell [88], the authors performed a more careful analysis of the effects of a magnetic field on the weak reactions which keep neutron and protons in thermal equilibrium considering, this time, also the direct effect of the magnetic field on the Universe expansion rate. Their final conclusions were in agreement with Greenstein's result.
The recent activity about the origin of magnetic fields during phase transitions in the early Universe (see Chap. 4) renewed the interest on the BBN bounds on primordial magnetic fields and induced several authors to reconsider the work of Matese and O'Connell and Greenstein. It is remarkable that after about twenty years and a large number of new astrophysical observations Greenstein's and Matese and O'Connell upper limit remains today roughly unchanged. Moreover, this is the case in spite of important developments of the BBN numerical computations codes.
We shall now abandon our historical approach to this section and proceed to give a more detailed description of the subject.
7 This issue was previously considered by Thorne [54]. Back.