3.1. The effect of a magnetic field on the neutron-proton conversion rate

The reactions which are responsible for the chemical equilibrium of neutrons and protons in the early Universe are the weak processes

	(3.2)
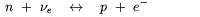
	(3.3)
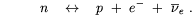
	(3.4)

In the absence of the magnetic field and in the presence of a heat-bath, the rate of each of the previous processes takes the generic form

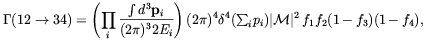
(3.5)

where p_i is the four momentum, E_i is the energy and f_i is the distribution function of the i-th particle species involved in the equilibrium processes. All processes (3.2, 3.3, 3.4) share the same amplitude determined by the standard electroweak theory.

The total neutrons to protons conversion rate is

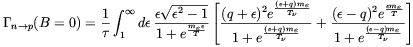
(3.6)

where q and are respectively the neutron-proton mass difference and the electron, or positron, energy, both expressed in units of the electron mass m_e. We neglect here the electron and neutrino electron chemical potentials as these are supposed to be small quantities during BBN [46]. The rate 1 / is defined by

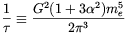
(3.7)

where G is the Fermi constant and g_A / g_V - 1.262. For T 0 the integral in Eq. (3.6) reduces to

(3.8)

and _n = / I is the neutron time-life.

The total rate for the inverse processes (p n) can be obtained reversing the sign of q in Eq. (3.6). It is assumed here that the neutrino chemical potential is vanishing (at the end of Sec. 3.4 it will also be discussed the case where such an assumption is relaxed). Since, at the BBN time temperature is much lower than the nucleon masses, neutrons and protons are assumed to be at rest.

As pointed out by Matese and O'Connell [86, 88], the main effect of a magnetic field stronger than the critical value B_c on the weak processes (3.2-3.4) comes-in through the effect of the field on the electron, and positron, wave function which becomes periodic in the plane orthogonal to the field [38]. As a consequence, the components of the electron momentum in that plane are discretized and the electron energy takes the form

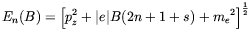
(3.9)

where we assumed B to be directed along the z axis. In the above, n denotes the Landau level, and s= ± 1 if, respectively, the electron spin is along or opposed to the field direction. Besides the effect on the electron dispersion relation, the discretization of the electron momentum due to the magnetic field has also a crucial effect on the phase-space volume occupied by these particles. Indeed, in the presence of a field with strength larger than B_c the substitution

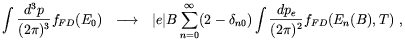
(3.10)

has to be performed [91]. Since we only consider here magnetic fields which are much weaker than the proton critical value (eB << m_p²), we can safely disregard any effect related to the periodicity of the proton wave function.

The squared matrix element for each of the reactions (3.2-3.4) is the same when the spin of the initial nucleon is averaged and the spins of the remaining particles are summed. Neglecting neutron polarization, which is very small for B < 10¹⁷ G, we have [86]

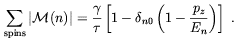
(3.11)

It is interesting to observe the singular behaviour when a new Landau level opens up (E_n = p_z). Such an effect is smoothed-out when temperature is increased [92].

Expressions (3.9) and (3.10) can be used to determined the rate of the processes (3.2-3.4) in a heat-bath and in the presence of an over-critical magnetic field. We start considering the neutron -decay. One finds

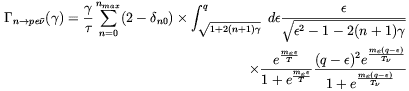
(3.12)

where B / B_c and n_max is the maximum Landau level accessible to the final state electron determined by the requirement p_z(n)² = q² - m_e² - 2n eB > 0 . It is noticeable that for > 1/2 (q² -1)² = 2.7 only the n = 0 term survives in the sum. As a consequence the -decay rate increases linearly with above such a value. The computation leading to (3.12) can be readily generalized to determine the rate of the reactions (3.2) and (3.3) for 0

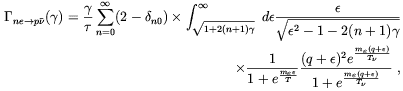
(3.13)

and

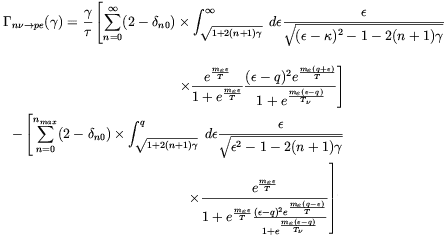
(3.14)

By using the well know expression of the Euler-MacLaurin sum (see e.g. Ref. [91]) it is possible to show that in the limit B 0 Eqs. (3.12-3.14) reduces to the standard expressions derived in the absence of the magnetic field ⁽⁸⁾

The global neutron to proton conversion rate is obtained by summing the last three equations

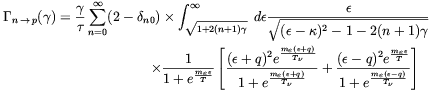
(3.15)

It is noticeable that the contribution of Eq. (3.12) to the total rate (3.15) is canceled by the second term of (3.14). As a consequence it follows that Eq. (3.15) does not depend on n_max and the n p conversion grows linearly with the field strength above B_c. From Fig. 3.1 the reader can observe that, in the range considered for the field strength, the neutron depletion rate drops quickly to the free-field when the temperature grows above few MeV's. Such a behaviour is due to the suppression of the relative population of the lowest Landau level when eB >> T².

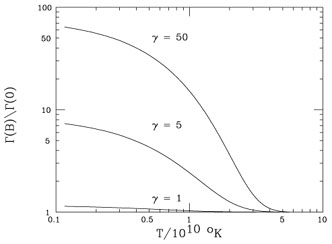
Figure 3.1. The neutron-depletion rate n p, normalized to the free-field rate, is plotted as a function of the temperature for several values of . From Ref. [94]

In the absence of other effects, the consequence of the amplification of _{n p} due to the magnetic field would be to decrease the relic abundance of ⁴He. In fact, a larger _n p implies a lower value of the temperature (T_F) at which the neutron to proton equilibrium ratio is frozen because of the expansion of the Universe. It is evident from (3.1) that the final value of (n/p) drops exponentially as T_F is increased. Furthermore, once n / p has been frozen, occasional neutron -decays can still reduce the relic neutron abundance [46]. As it follows from Eq. (3.12), the presence of a strong magnetic field accelerates the process which may give rise to a further suppression of the n/p ratio. In practice, however, neutron decay takes place at a times when the magnetic field strength has already decreased significantly due to the Universe expansion so that the effect is negligible.

The result of Matese and O'Connell has been confirmed by Cheng et al. [93] and by Grasso and Rubinstein [94]. Among other effects, the authors of Ref. [94] considered also QED and QCD corrections in the presence of strong magnetic fields. In principle these corrections may not be negligible in the presence of over-critical magnetic fields and their computation requires a proper treatment. In order to give to the reader a feeling of the relevance of this issue, we remind him the wrong result which was derived by O'Connell [39] by neglecting QED radiative correction to the electron Dirac equation in the presence of a strong magnetic field. By assuming the electron anomalous magnetic moment to be independent on the external field O'Connell found

(3.16)

For B > (4 / ) B_c this expression give rise to negative values of the ground state energy which, according to O'Connell, is the manifestation of the instability of the vacuum to spontaneous production of electron-positron pairs. This conclusion, however, is in contradiction with standard electrodynamics from which we know that a constant magnetic field cannot transfer energy. This problem was solved by several authors (see e.g. Ref. [37]) by showing that by properly accounting for QED radiative corrections to the Dirac equation no negative value of the electron energy appear. The effect can be parametrized by a field dependent correction to the electron mass, m_e m_e + M, where

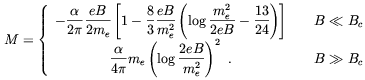
(3.17)

Such a correction was included in Refs. [94, 95]. It is interesting to observe that although pair production cannot occur at the expense of the magnetic field, this phenomenon can take place in a situation of thermodynamic equilibrium where pair production can be viewed as a chemical reaction e⁺ + e^- <-> , the magnetic field playing the role of a catalysts agent [96]. We will return on this issue in Sec. 3.3.

Even more interesting are the corrections due to QCD. In fact, Bander and Rubinstein showed that in the presence of very strong magnetic fields the neutron-proton effective mass difference q becomes [97] (for a more detailed discussion of this issue see Chap. 5)

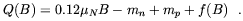
(3.18)

The function f(B) gives the rate of mass change due to colour forces being affected by the field. µ_N is the nucleon magnetic moment. For nucleons the main change is produced by the chiral condensate growth, which because of the different quark content of protons and neutrons makes the proton mass to grow faster [97]. Although, as a matter of principle, the correction to Q should be accounted in the computation of the rates that we reported above, in practice however, the effect on the final result is always negligible. More subtle it is the effect of the correction to Q on the neutron-to-proton equilibrium ratio. In fact, as it is evident from Eq. (3.1), in this case the correction to Q enters exponentially to determine the final neutron-to-proton ratio. However, the actual computation performed by Grasso and Rubinstein [94] showed that the effect on the light element abundances is sub-dominant whenever the field strength is smaller than 10¹⁸ Gauss.

---

⁸ For a different approach see Ref. [93]. Back.