3.4. Derivation of the constraints

In order to account for all the effects discussed in the previous sections, the use of a numerical analysis is required. Usually, this is done by modifying properly the famous BBN numerical code developed by Wagoner and improved by Kawano [100]. After some discussion around the relative importance of the different effects, the results of different groups have converged to a common conclusion: the most relevant effect of a cosmological magnetic field on BBN is that produced by the energy density of the field on the Universe expansion rate. This is in qualitative agreement with the early result of Greenstein [89]. From a more quantitative point of view, however, the effect of the magnetic field on the electron thermodynamics cannot be totally neglected. In fact, it was showed in [95] that such an effect produces sizable changes in the relic abundance of ⁴He, Deuterium and ³He (see e.g. Fig. 3.2 for the ⁴He relic abundance prediction). As a consequence, we think that the effect of the magnetic field on the BBN cannot be simply parameterized in terms of a contribution to the effective number of neutrino species. Although, in this respect, a different conclusion was reached in [98, 101] it should be noted that, differently from [95], in those papers only approximate expressions for the electron thermodynamic quantities in the presence of a strong magnetic field were used. Such an approximation may be not justified when eB T².

According to the standard procedure, the upper limit on the strength of the cosmological magnetic field was obtained in [94, 95, 102] by comparing the numerically predicted relic abundance of ⁴He with the observational upper limit. In [95] however, the information about Deuterium and ³He was also used. In fact, since the effective value of is also affected by the magnetic field, was chosen in the actual numerical simulation so to saturate the predicted value of D + ³He / H to the observational upper limit. This choice assured the minimal predicted abundance of ⁴He for each considered value of B.

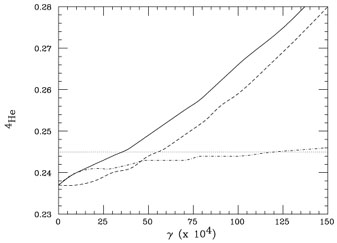
Figure 3.2. The 4He predicted abundance is represented in function of the parameter , considered at T = 109 oK, in three different cases: only the effect of the magnetic field energy density is considered (dashed line); only the effect of the field on the electron statistics is considered (dotted-dashed line); both effects are considered (continuous line). The dotted line represents the observational upper limit. From Ref. [95]

By fixing N = 3, requiring Y_P < 0.245 and D + ³He / H < 1.04 × 10^-4 Grasso and Rubinstein derived the upper limit

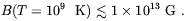
(3.31)

Similar results has been obtained by the authors of Refs. [101, 103].

It is useful to remind to the reader under which assumptions the previous limit has been derived. They are the following.

1. Universe dynamics was assumed to be well described by Friedman-Robertson-Walker metric. In other words we are assuming that the magnetic field does not lead to a sizeable anisotropic component in the Universe expansion ⁽⁹⁾.
2. The effective number of neutrino species is three. This means, for example, that if neutrinos are of Dirac type their mass and magnetic moment are negligible. This in order do not populate right handed degree of freedom by the magnetic dipole interaction of the neutrinos with the field.
3. The neutrino chemical potential is negligible.
4. Fundamental physical constants are equal to their present time values (for a discussion on this issue see Ref. [104]).

Some of these assumptions will be relaxed in the following part of this chapter.

In order to translate our limit (3.31) into a bound on the magnetic field at the time of galaxy formation some caution is required. If we just assume that the magnetic field re-scales adiabatically with the Universe expansion, according to Eq. (3.23), the BBN limit reads

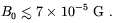
(3.32)

We should keep in mind, however, that in this case we are neglecting any possible nonadiabatic evolution of the magnetic field as that which could be induced by a non-trivial topology of the field. Even assuming an adiabatic evolution, we note that the limit (3.32) cannot be directly interpreted as a limit on the progenitor of galactic magnetic fields. The reason for that is that BBN probes magnetic fields on scales of the order of the horizon radius at BBN time (the Hubble comoving radius at BBN time is ~ 100 pc) which are much smaller than typical protogalaxy sizes (~ 1-10 Mpc). Therefore, if cosmic magnetic field are tangled on scales smaller than the protogalactic size, the progenitor magnetic field has to be interpreted as a proper average of smaller flux elements. Clearly, the result of such an average will depend on the statistical properties of the random magnetic field. If the field vector were to perform a random walk in 3d volume, the scaling would be B(L) <B>_{rms, L} ~ N^-3/2 [105], where L₀ is the comoving coherence length of the magnetic field and N = L / L₀ is the number of steps. An argument based on the statistical independence of conserved flux elements gives B(L) ~ N^-1 [106], whereas another argument based on the statistical independence of the field in neighboring cells predicts B(L) ~ N^-1/2 [107]. Adopting a phenomenological point of view, one may just write that the rms field computed on the scale L at the time t is [108]

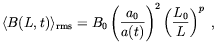
(3.33)

where p is an unknown parameter (p = 3/2, 1, 1/2 respectively in the three cases discussed in the above). The meaning of B₀ is now understood as B₀ = lim_L B(L, t₀) ⁽¹⁰⁾. If, for example, we adopt the value p = 1 and assume L₀ = 100 pc, the limit (3.32) implies

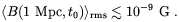
(3.34)

Therefore, although the BBN bound is much more stringent than what is usually claimed in the literature, it cannot exclude a primordial origin of galactic magnetic fields by the adiabatic compression of the field lines.

For the same reasons which we have explained in the above, BBN limits on primordial magnetic fields cannot be directly compared with bounds derived from the analysis of CMBR anisotropies. In fact, unless the magnetic fields is uniform through the entire Universe, CMBR offers a probe of magnetic fields only on comoving scales which are much larger than the horizon radius at BBN time.

We shall now consider how the previous limits changes by relaxing one of the assumptions under which the constraint (3.31) has been derived, namely that related to the neutrino chemical potential. The effects of a possible neutrino-antineutrino asymmetry in this context has been recently considered by Suh and Mathews [110]. This issue is interesting since several recent leptogenesis scenarios predict the formation of such asymmetry during the radiation era. It is well know that even in the absence of a primordial magnetic field a non-vanishing neutrino chemical potential can affect the predictions of BBN (see Ref. [111] and references therein). In fact, a degeneracy of the electron neutrino changes both the weak reaction rates and the neutron-to-proton equilibrium ratio, whereas a degeneracy in any of the neutrino species modifies the expansion rate of the Universe. Clearly, the presence of any of these effects would affect the BBN limit on the strength of a primordial magnetic field. Suh and Mathews found that if the limit is B₀ 5.8 × 10^-7 G with _e µ_e / T_e = 0 (in good agreement with the limit (3.32)), it becomes B₀ 2.8 × 10^-6 Gauss if _e µ_e / T_e = 0.15. Therefore, we see that in the presence of phenomenologically acceptable values of the neutrino chemical potential the BBN constraint on the magnetic field can be considerably relaxed.

⁹ BBN in the presence of anisotropic Universe, possibly due to a homogeneous cosmic magnetic field, has been considered by Thorne [54]. Back.

¹⁰ A detailed discussion about average procedures of tangled magnetic fields can be found in Ref. [109]. Back.