3.3. The effect on the electron thermodynamics

In the above we discussed how the phase-space of electrons and positrons is modified by the presence of strong magnetic fields and how this effect changes the weak processes rates. The consequences of the variation of the electron phase-space, however, go well beyond that effect. Electron and positron thermodynamics functions will also be affected. In fact, by applying the prescription (3.10), we find that the number density, the energy density and the pressure of the electron-positron gas are now given by

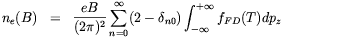
	(3.26)
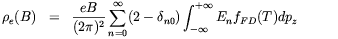
	(3.27)
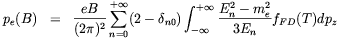
	(3.28)

where

(3.29)

is the Fermi-Dirac distribution function, and E_n(p_z) is given by (3.9). As for the case of the weak processes rates, it is possible to show that Eqs. (3.26-3.28) reduce to the their well know standard from in the limit B 0 (see e.g. Ref. [98]).

Numerical computations [94] show that, for small T, _e grows roughly linearly with B when B > B_c. This effect is mainly due to - 1) the reduction, for each Landau level, of the area occupied by the cyclotron motion of the electron in plane perpendicular to the field; 2) the growth of the energy gap among the lowest Landau level and the n > 0 levels, which produces an overpopulation of the lowest Landau level. The first effect is the dominant one. The net number density and the pressure of the electron-positron gas follow a similar behaviour. As we already noted in Sec. 3.1, the energy cost of producing the electron-positron pairs excess cannot be paid by the magnetic field which is supposed to be static. Rather, the "power bill" is paid from the heat-bath, or better, from its photon component [96, 99]. Especially in the context of BBN this point is quite relevant since the energy transfer from the photons to the lowest Landau level of the electron-positron gas will affect the expansion rate of the Universe, its cooling rate and the effective baryon-to-photon ratio [94, 95, 98]. We start discussing the first two effects. We observe that the growth of the electron and positron energy density, due to the presence of the magnetic field, gives rise to a faster expansion rate of the Universe. This point was first qualitatively discussed by Matese and O'Connell [87] and recently analyzed in more detail by Grasso and Rubinstein [94]. The time-temperature relation will also be modified. The relevance of latter effect has been first showed by Kernan, Starkman and Vachaspati [98] by solving numerically the relation

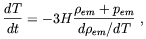
(3.30)

where _{em e} + and p_em p + p_e are the energy density and the pressure of the electromagnetic component of the primordial heat-bath. In agreement with our previous considerations, Eq. (3.30) has been obtained by imposing energy conservation of the electromagnetic component plasma.

For small values of the ratio eB/T², the most relevant effect of the magnetic field enters in the derivative d_em / dT that is smaller than the free field value. This effect can be interpreted as a delay in the electron-positron annihilation time induced by the magnetic field. This will give rise to a slower entropy transfer from the electron-positron pairs to the photons, then to a slower reheating of the heat bath. In fact, due to the enlarged phase-space of the lowest Landau level of electrons and positrons, the equilibrium of the process e⁺ e^- <-> is shifted towards its left side. Below we will discuss as this effect has a clear signature on the deuterium and ³He predicted abundances. Another point of interest is that the delay in the e⁺ e^- annihilation causes a slight decrease in the T / T ratio with respect to the canonical value, (4/11)^1/3 [98].

The delay in the entropy transfer from the e⁺ e^- gas to the heat-bath induces also an increment in the value of baryon-to-photon ratio . In the absence of other effects a larger value of would induce smaller relic abundances of Deuterium and ³He. This effect, was first predicted in the Refs. [94, 95], Furthermore, it is interesting to observe that in the case the primordial magnetic field is inhomogeneous and it is confined in finite volume regions where its strength exceed the cosmic mean value (e.g. flux tubes), this effect may give rise to spatial variation in the relic element abundances.