3.5. Neutrino spin-oscillations in the presence of a magnetic field

It is interesting to consider how the limit obtained in the previous section changes if neutrinos carry non-standard properties which may change the effective neutrino number during BBN. We are especially interested here to the possibility that neutrinos carry non-vanishing masses and magnetic moments. If this is the case, the dipole interaction of the neutrinos with the magnetic field may give rise to spin-oscillations of the neutrinos, i.e. periodic conversion of a helicity state into another. In the case of Dirac neutrinos, this phenomenon may have crucial consequences for BBN. In fact, spin-oscillation can populate the right-handed helicity state of the neutrino which, being practically sterile (for m << T) to weak interactions, would otherwise play no effective role. By adding a new degree of freedom to the thermal bath, such an effect may produce dangerous consequences for the outcome of BBN. This problem was first pointed-out by Shapiro and Wasserman [112] and, independently, by Lynn [113] who used the argument to put a constraint on the product of the magnetic field with the neutrino magnetic moment. In both works, however, the important role played by neutrino refractive properties determined by the neutrino collective interaction with the heat-bath, as well as that played by neutrino scattering with leptons, were disregarded. A more complete treatment was developed by Fukugita et al. [114]. They showed that the conditions under which the neutrino wrong-helicity state can be effectively populated are the following:

1. the spin-oscillation frequency E_magn = 2 µ B has to exceed the Universe expansion rate;
2. since neutrino scattering destroy the phase relationship between the left-handed and right-handed helicity states, E_magn has to be larger than the scattering rate;
3. since the refractive indices for left-handed and right-handed states, n_L and n_R, are not equal, oscillations can occur only if

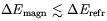
   (3.35)

   where E_refr (n_L - n_R) E.

The BBN is affected only if such conditions are simultaneously satisfied at some temperature T_osc in the range T_dec T_osc T_QCD where T_dec 1 MeV is the neutrino decoupling temperature and T_QCD 200 MeV. Note that in the case right-handed neutrinos decouples before the QCD phase transition, the huge amount of entropy which is expected to be released during this transition would dilute their relative abundance so to prevent any effect on the BBN. From the previous considerations the authors of Ref. [114] derived the limit

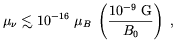
(3.36)

where µ_B is the Bohr magneton. The work of Fukugita et al. has been reconsidered by several authors. For example, Enqvist, Olesen and Semikoz [115], improved the previous analysis by considering the effect of the neutrino refractive properties on the left-right transition probability. Elmfors, Grasso and Raffelt [116] accounted for the effect of the magnetic field on the neutrino refractive properties and used an improved treatment of neutrino collisions. First of all, Elmfors et al. noted that by affecting the thermodynamics properties of the electromagnetic component of the heat-bath (see Sec. 3.3) a strong magnetic field changes also the neutrino potentials. This may have relevant consequences both for neutrino spin-oscillations and flavour oscillations in a magnetized medium [117]. The interplay between spin-oscillations and collisions was then accounted in Ref. [116] by means of the following evolution equation [118]

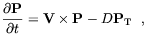
(3.37)

where P is the neutrino polarization vector and P_T is its transverse component respect to the neutrino direction of motion. V is a vector of effective magnetic interaction energies which can be decomposed into its transverse and longitudinal components

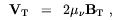
	(3.38)
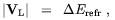
	(3.39)

where µ is the neutrino magnetic moment and [116]

(3.40)

is the left-right neutrino energy difference in the magnetized medium ⁽¹¹⁾. It is worthwhile to note that in Eq. (3.40) the expression (3.27) has to be used for _e(B). As we wrote above, collisions destroy the phase coherence between the left-handed and right-handed component of a neutrino state, which amounts to a damping of the transverse part P_T of the polarization vector. The main contribution to the damping rate D comes from neutrino elastic and inelastic scattering with leptons and equals half the total collision rate of the left-handed component [121]. In the early Universe at T ~ 1 MeV one finds:

(3.41)

where f_D is a order one numerical factor. Inserting the previous expressions in Eq. (3.37) it is easy to derive the neutrino depolarization rate _depol. In the small mixing angle limit,

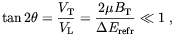
(3.42)

one finds

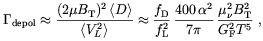
(3.43)

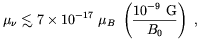
(3.44)

which is not too different from the limit (3.36) previously found by the authors of Ref. [114]. Limits on µ were also found by the authors of Refs. [108, 122] who considered the case of random magnetic fields.

In principle, right-handed neutrinos could also be populated by direct spin-flip interactions mediated by virtual photons produced by scattering on charged particles or by annihilation processes [123], as well as by the interaction with small scale magnetic fields produced by thermal fluctuations [124]. In practice, however, bounds on µ from a possible large scale magnetic field are found to be more stringent even for very weak magnetic fields. The most stringent upper limit on Dirac type neutrino magnetic moment with mass m < 1 MeV, comes from stellar evolution considerations. It is µ 3 × 10^-12µ_B [125, 126]. It is interesting to observe that if one of the neutrinos saturate this limit, Eq. (3.44) implies the following quite stringent bound on the present time cosmic magnetic field, B₀ 10^-13 G.

In the particle physics standard model, neutrinos have no magnetic dipole moment. However, if the neutrino has a Dirac mass m, radiative corrections automatically give rise to a finite dipole moment [113]

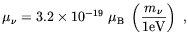
(3.45)

even without invoking any further extension of the standard model beside that required to account for the finite neutrino mass. On the basis of this consideration Enqvist et al. [127] derived the following upper limit for the present time local magnetic field

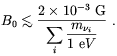
(3.46)

Clearly, this limit cannot compete with the constraint derived in the previous section.

Spin oscillations in the presence of twisted primordial magnetic fields (i.e. magnetic field with a nonvanishing helicity, see Sec. 1.4) have been considered by Athar [128]. Athar showed that in such a situation the left-right conversion probabilities for neutrino and antineutrinos may be different. This result may open the interesting possibility that a neutrino-antineutrino asymmetry may be generated during the big-bang by a preexisting non trivial topology of a primeval magnetic field. As we shall see in Sec. 4.4, the production of a net magnetic helicity of the Universe is indeed predicted by some models.

It is also interesting to speculate on the effects when the number of dimensions change, and these are large [129]. In fact BBN is one of the most serious objections to this idea, together with the background diffuse gamma radiation [130]. Detailed studies of effects of magnetic fields in these scenarios are not available yet.

¹¹ For a computation of the neutrino refractive properties in a magnetized medium see also Refs. [119, 120]. Back.

¹² Note that in Ref. [116] B₀ was defined as the magnetic field at BBN time. Back.