4.2. Magnetic fields from the quark-hadron phase transition

It is a prediction of Quantum-Chromo-Dynamics (QCD) that at some very high temperature and/or density strongly interacting matter undergoes a deconfinement transition, where quark/gluon degrees of freedom are "melted-out" from hadrons. In the early Universe, due to the cosmological expansion, the process proceeds in the opposite direction starting from a "quark-gluon plasma" which at some critical temperature T_QCD condenses into colorless hadrons [137]. Lattice computations suggest that the QCD phase transition (QCDPT) is a first-order phase transition taking place at T_QCD ~ 150 MeV [138]. Typically a first-order phase transition takes place by bubble nucleation. As the temperature supercools below T_QCD, sub-critical bubbles containing the hadronic phase grow as burning deflagration fronts releasing heat in the quark-gluon plasma in the form of supersonic shock fronts. When the shock fronts collide they reheat the plasma up to T_QCD stopping bubble grow. Clearly, up to this time, the transition is an out-of-equilibrium process. Later on, the growth of newly nucleated bubbles proceeds in thermal equilibrium giving rise to the, so-called, coexistence phase. The latent heat released by these bubbles compensate for the cooling due to the Universe expansion keeping temperature at T_QCD. The transition ends when expansion wins over and the remaining quark-gluon plasma pockets are hadronized.

The first step of the magnetogenesis scenario at the QCDPT proposed by Quashnock, Loeb and Spergel [139] consists in the formation of an electric field behind the shock fronts which precede the expanding bubbles. This is a consequence of the baryon asymmetry, which was presumably already present and which makes the baryonic components of the primordial plasma positively charged. At the same time, the leptonic component must be negatively charged to guarantee the Universe charge neutrality. The other crucial ingredient of the mechanism is the difference in the equation of state of the baryonic and leptonic fluids. As a consequence, the strong pressure gradient produced by the passage of the shock wave gives rise to a radial electric field behind the shock front. Such a generation mechanism is usually known as a battery. Quashnock et al. gave the following estimate for the strength of the electric field

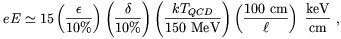
(4.2)

where represents the ratio of the energy densities of the two fluids, ( p / p) is the pressure gradient and l is the average distance between nucleation sites.

Small scale magnetic fields are generated by the electric currents induced by the electric fields. These fields, however, live on a very small scale (<< ) and presumably they are rapidly dissipated. Phenomenologically more interesting fields should be produced when the shock fronts collide giving rise to turbulence and vorticity on a scales of order . Magnetic fields are produced on the same scale by the circulation of electric fields of magnitude given by Eq. (4.2). Then, using standard electrodynamics, Quashnock et al. found that the magnetic field produced on the scale ~ 100 cm has a magnitude

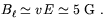
(4.3)

Following the approach which was first developed by Hogan [105], the magnetic field on scales L >> can be estimated by performing a proper volume average of the fields produced by a large number of magnetic dipoles of size randomly oriented in space. Such an average gives

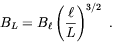
(4.4)

After the QCDPT the magnetic field evolves according to the frozen-in law (1.24). It is straightforward to estimate the magnetic field strength at the recombination time on a given scale L. The smaller conceivable coherence length is given by the dissipation length at that time which, following the argument already described in Sec. 1.4, is found to be L_diss(t_rec) 5 × 10¹⁰ cm, corresponding to 1 A.U. at present time. On this scale the magnetic field produced at the QCDPT is 2 × 10^-17 G. This small strength is further dramatically suppressed if one considers scales of the order of the galactic size ~ 10 kpc. Therefore, it looks quite unplausible that the magnetic fields generated by this mechanism could have any phenomenological relevance even if the galactic dynamo was effective.

According to a more recent paper by Cheng and Olinto [140] stronger fields might be produced during the coexistence phase of the QCDPT. The new point raised by the authors of Ref.[140] is that even during such equilibrium phase a baryon excess build-up in front of the bubble wall, just as a consequence of the difference of the baryon masses in the quark and hadron phases. According to some numerical simulations [141], this effect might enhance the baryon density contrast by few orders of magnitude. Even more relevant is the thickness of the charged baryonic layer which, being controlled by baryon diffusion, is ~ 10⁷ fm rather than the microphysics QCD length scale ~ 1 fm. In this scenario magnetic fields are generated by the peculiar motion of the electric dipoles which arises from the convective transfer of the latent heat released by the expanding bubble walls. The field strength at the QCDPT time has been estimated by Cheng and Olinto to be as large as

(4.5)

on a maximal coherence length l_coh H^-1_QCD. Once again, by assuming frozen-in evolution of the field, one can determine present time values:

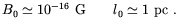
(4.6)

Using Eq. (105) Cheng and Olinto found that on the galactic length scale B(kpc) 10^-20 G which may have same phenomenological relevance if the galactic dynamo is very effective.

In a following work Sigl, Olinto and Jedamzik [142] investigated the possible role that hydrodynamic instabilities produced by the expanding bubble walls may have in generating strong magnetic fields. Although is not clear whether these instabilities can really develop during the QCDPT, Sigl at al. claimed that this phenomenon is not implausible for a reasonable choice of the QCDPT parameters. By taking into account the damping due to the finite viscosity and heat conductivity of the plasma, the authors of Ref.[142] showed that the instability may grow non-linearly producing turbulence on a scale of the order of the bubble size at the percolation time. As a consequence, a MHD dynamo may operate to amplify seed magnetic fields and equipartition of the magnetic field energy with the kinetic energy may be reached. If this is the case, magnetic fields of the order of 10^-20 G may be obtained at the present time on a very large scale ~ 10 Mpc. Larger fields may be obtained by accounting for an inverse cascade (see Sec. 1.4). In the most optimistic situation in which the magnetic field was produced having maximal helicity at the QCDPT and equipartion between magnetic and thermal energy was realized at that time, Eqs. (1.34, 1.35) for the time evolution of the rms field strength and coherence length apply. By substituting in such equations the initial scale l(T_i) ~ r_H(T_QCD) ~ 30 km, and B_rmrms(T_i) ~ 10¹⁷ G, one finds the present time values

(4.7)

Remarkably, we see that in this optimistic case no dynamo amplification is required to explain galactic, and probably also cluster, magnetic fields.