4.3. Magnetic fields from the electroweak phase transition

4.3.1. Magnetic fields from a turbulent charge flow

Some of the ingredients which may give rise to magnetogenesis at the QCDPT may also be found at the electroweak phase transition (EWPT). As for the case of the QCDPT, magnetogenesis at the weak scale seems to require a first order transition. Although recent lattice computations performed in the framework of the standard electroweak theory [143] give a strong evidence against a first order transition, this remains a viable possibility if supersymmetric extension of the standard model are considered [144]. It is noticeable that a first order EWPT is also required for the successful realization of the electroweak baryogenesis scenario [145]. Indeed, as we shall see in the rest of this review, this is only one among several common aspects of baryogenesis and magnetogenesis.

According to Baym, Bödeker and McLerran [146] strong magnetic fields can be generated by a first order EWPT ⁽¹³⁾ via a dynamo mechanism. In this scenario seed fields are provided by random magnetic field fluctuations which are always present on a scale of the order of a thermal wavelength ⁽¹⁴⁾. The amplification of such seed fields proceeds as follows. When the Universe supercooled below the critical temperature (T_c ~ 100 GeV) the Higgs field locally tunneled from the unbroken SU(2) × U(1)_Y phase to the broken U(1)_em phase. The tunneling gave rise to the formation of broken phase bubbles which then expanded by converting the false vacuum energy into kinetic energy. Although the bubble wall velocity is model dependent, one can find that for a wide range of the standard model parameters the expansion is subsonic (deflagration) which give rise to a supersonic shock wave ahead of the burning front. As the shock fronts collided turbulence should have formed in the cone associated with the bubble intersection. The Reynold number for the collision of two bubbles is

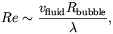
(4.8)

where v_fluid~ v_wall ~ 10^-1 is the typical fluid velocity, R_bubble is the size of a bubble at the collision time and is the scattering length of excitations in the electroweak plasma. The typical size of a bubble after the phase transition is completed is in the range

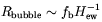
(4.9)

where

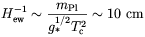
(4.10)

is the size of the event horizon at the electroweak scale, m_Pl is the Planck mass, g_*~ 10² is the number of massless degrees of freedom in the matter, and the fractional size f_b is ~ 10^-2-10^-3. The typical scattering length of excitations in the plasma is of order

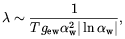
(4.11)

where _w is the fine structure constant at the electroweak scale, and g_ew ~ g_* is the number of degrees of freedom that scatter by electroweak processes. By substituting these expressions Baym et al. found

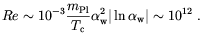
(4.12)

Such a huge Reynolds number means that turbulence fully develops at all scales smaller than R_bubble. Since conductivity is expected to be quite large at that time [49], magnetic fields followed the fluid motion so that a strong magnetic turbulence should also have been produced. In such a situation it is known that the kinetic energy of the turbulent flow is equipartitioned with the magnetic field energy. Therefore

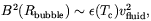
(4.13)

where (T_c) ~ g_* T_c⁴ is the energy density of the electroweak plasma.

In order to estimate the magnetic field strength on scale larger than R_bubble, Baym et al. treated the large scale field as a superposition of the field of dipoles with size R_bubble. This is similar to what done by other authors [105, 140] (see what we wrote above for the QCDPT) apart for the fact that Baym et al. used a continuum approximation for the distribution of dipoles rather than to assume a random walk of the field lines. The density ⁱ(r) of dipoles pointing in the i-th direction was assumed to be Gaussianly distributed. This implies the following correlation functions for the density of dipoles

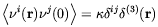
(4.14)

and for the magnetic field

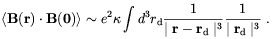
(4.15)

The logarithmic divergence of the integral in these regions is cut off by the size of the typical dipole, f_b H^-1_ew, so that for r >> f_b H^-1_ew,

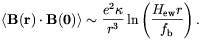
(4.16)

By using this expression and the equipartition relation (4.13) one finds that the strength of B² measured by averaging on a size scale R is

(4.17)

This result can be better expressed in terms of the ratio r of <B²> to the energy in photons which is a constant during Universe expansion in the absence of flux diffusion. From Eqs. (4.17) one gets

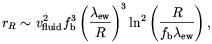
(4.18)

where _ew is the Hubble radius at the electroweak phase transition (~ 1 cm) times the scale factor, T_c / T, where T is the photon temperature.

From the previous results the authors of Ref. [146] estimated the average magnetic field strength at the present time. This is

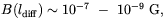
(4.19)

where l_diff ~ 10 AU is present time diffusion length, and

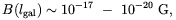
(4.20)

on the galactic scale l_gal ~ 10⁹ AU.

¹³ At the time the paper by Baym et al. was written, a first order EWPT was thought to be compatible with the standard model. Therefore all computation in [146] were done in the framework of that model. Back.

¹⁴ It is worthwhile to observe here that thermal fluctuation in a dissipative plasma can actually produce stochastic magnetic fields on a scale larger than the thermal wavelength [147, 148]. Back.