


4.3.2. Magnetic fields from Higgs field equilibration
In the previous section we have seen that, concerning the generation of magnetic fields, the QCDPT and the EWPT share several common aspects. However, there is one important aspect which makes the EWPT much more interesting than the QCDPT. In fact, at the electroweak scale the electromagnetic field is directly influenced by the dynamics of the Higgs field which drives the EWPT.
To start with we remind that, as a consequence of the Weinberg-Salam theory, before the EWPT is not even possible to define the electromagnetic field, and that this operation remains highly non-trivial until the transition is completed. In a sense, we can say that the electromagnetic field was "born" during the EWPT. The main problem in the definition of the electromagnetic field at the weak scale is the breaking of the translational invariance: the Higgs field module and its SU(2) and UY(1) phases take different values in different positions. This is either a consequence of the presence of thermal fluctuations, which close to Tc are locally able to break/restore the SU(2) × UY(1) symmetry or of the presence of large stable domains, or bubbles, where the broken symmetry has settled.
The first generalized definition of the electromagnetic field in the presence of a non-trivial Higgs background was given by t'Hooft [149] in the seminal paper where he introduced magnetic monopoles in a SO(3) Georgi-Glashow model. t'Hooft definition is the following
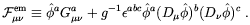
| (4.21) |
In the above G
aµ

 W
aµ -
W
aµ -
 W
a
W
a , where
, where
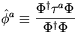
| (4.22) |
( a are the Pauli
matrices) is a unit isovector which
defines the "direction" of the Higgs field in the SO(3)
isospace (which coincides with SU(2)) and
(Dµ
a are the Pauli
matrices) is a unit isovector which
defines the "direction" of the Higgs field in the SO(3)
isospace (which coincides with SU(2)) and
(Dµ )a =
)a =
 µ
µ a
+ g
a
+ g  abc
Wµb
abc
Wµb c,
where Wµb are the gauge fields
components in the adjoint
representation. The nice features of the definition
(4.21)
are that it is gauge-invariant and it reduces to the standard
definition of the electromagnetic field tensor if a gauge rotation
can be performed so to have
c,
where Wµb are the gauge fields
components in the adjoint
representation. The nice features of the definition
(4.21)
are that it is gauge-invariant and it reduces to the standard
definition of the electromagnetic field tensor if a gauge rotation
can be performed so to have
 a =
-
a =
-  a3
(unitary gauge). In some models, like that considered by t'Hooft, a
topological obstruction may prevent this operation to be possible
everywhere. In this case singular points (monopoles) or lines
(strings) where
a3
(unitary gauge). In some models, like that considered by t'Hooft, a
topological obstruction may prevent this operation to be possible
everywhere. In this case singular points (monopoles) or lines
(strings) where  a = 0 appear which become the source of
magnetic fields. t'Hooft result provides an existence proof of magnetic
fields produced by non-trivial vacuum configurations.
a = 0 appear which become the source of
magnetic fields. t'Hooft result provides an existence proof of magnetic
fields produced by non-trivial vacuum configurations.
The Weinberg-Salam theory, which is based on the SU(2) × UY(1) group representation, does not predict topologically stable field configurations. We will see, however, that vacuum non-topological configurations possibly produced during the EWPT can still be the source of magnetic fields.
A possible generalization of the definition (4.21) for the Weinberg-Salam model was given by Vachaspati [106]. It is
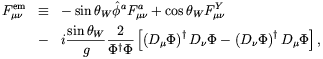
| (4.23) |
Dµ =
 µ
- i[(g) / 2]
µ
- i[(g) / 2]
 a
Wµa -i[(g') / 2]
Yµ.
a
Wµa -i[(g') / 2]
Yµ.
This expression was used by Vachaspati to argue that magnetic
fields should have been produced during the EWPT. Synthetically,
Vachaspati argument is the following. It is known that well below
the EWPT critical temperature Tc the minimum energy
state of the Universe corresponds to a spatially homogeneous vacuum in
which  is covariantly
constant, i.e.
D
is covariantly
constant, i.e.
D
 =
Dµ
=
Dµ
 a =
0. However, during the EWPT, and
immediately after it, thermal fluctuations give rise to a finite
correlation length
a =
0. However, during the EWPT, and
immediately after it, thermal fluctuations give rise to a finite
correlation length  ~
(eTc)-1. Therefore, there are
spatial variations both in the Higgs field module
|
~
(eTc)-1. Therefore, there are
spatial variations both in the Higgs field module
| | and in its SU(2)
and U(1)Y phases which take random
values in uncorrelated regions
(15). It was
noted by Davidson
[150]
that gradients in the radial
part of the Higgs field cannot contribute to the production of
magnetic fields as this component is electrically neutral. While this
consideration is certainly correct, it does not imply the failure
of Vachaspati argument. In fact, the role played by
the spatial variations of the SU(2) and U(1)Y
"phases" of the the Higgs field cannot be disregarded.
It is worthwhile to observe that gradients of these phases are not a
mere gauge artifact as they correspond to a nonvanishing kinetic
term in the Lagrangian. Of course one can always rotate Higgs
fields phases into gauge boson degrees of freedom (see below) but
this operation does not change
Femµ
| and in its SU(2)
and U(1)Y phases which take random
values in uncorrelated regions
(15). It was
noted by Davidson
[150]
that gradients in the radial
part of the Higgs field cannot contribute to the production of
magnetic fields as this component is electrically neutral. While this
consideration is certainly correct, it does not imply the failure
of Vachaspati argument. In fact, the role played by
the spatial variations of the SU(2) and U(1)Y
"phases" of the the Higgs field cannot be disregarded.
It is worthwhile to observe that gradients of these phases are not a
mere gauge artifact as they correspond to a nonvanishing kinetic
term in the Lagrangian. Of course one can always rotate Higgs
fields phases into gauge boson degrees of freedom (see below) but
this operation does not change
Femµ which is a
gauge-invariant quantity. The contribution to the electromagnetic
field produced by gradients of
which is a
gauge-invariant quantity. The contribution to the electromagnetic
field produced by gradients of
 a can be
readily
determined by writing the Maxwell equations in the presence of an
inhomogeneous Higgs background
[151]
a can be
readily
determined by writing the Maxwell equations in the presence of an
inhomogeneous Higgs background
[151]
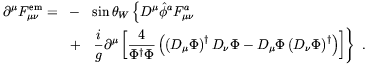
| (4.24) |
Even neglecting the second term on the righthand side of
Eq. (4.24), which depends on the definition of
Femµ in a Higgs inhomogeneous background (see
below), it is evident
that a nonvanishing contribution to the electric 4-current arises
from the covariant derivative of
in a Higgs inhomogeneous background (see
below), it is evident
that a nonvanishing contribution to the electric 4-current arises
from the covariant derivative of
 a. The physical
meaning of this contribution may look more clear to the reader if
we write Eq. (4.24) in the unitary gauge
a. The physical
meaning of this contribution may look more clear to the reader if
we write Eq. (4.24) in the unitary gauge
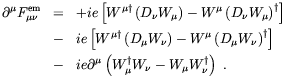
| (4.25) |
Not surprisingly, we see that the electric currents produced by Higgs field equilibration after the EWPT are nothing but W boson currents.
Since, on dimensional grounds,
D
 ~ v /
~ v /
 where
v is the Higgs field vacuum expectation value, Vachaspati
concluded that magnetic fields (electric fields were supposed to
be screened by the plasma) should have been produced at the EWPT
with strength
where
v is the Higgs field vacuum expectation value, Vachaspati
concluded that magnetic fields (electric fields were supposed to
be screened by the plasma) should have been produced at the EWPT
with strength
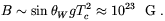
| (4.26) |
Of course these fields live on a very small scale of the order of
 and in order to determine
fields on a larger scale
Vachaspati claimed that a suitable average has to be performed
(see return on this issue below in this section).
and in order to determine
fields on a larger scale
Vachaspati claimed that a suitable average has to be performed
(see return on this issue below in this section).
Before discussing averages, however, let us try to understand better the nature of the magnetic fields which may have been produced by the Vachaspati mechanism. We notice that Vachaspati's derivation does not seem to invoke any out-of-equilibrium process and indeed the reader may wonder what is the role played by the phase transition in the magnetogenesis. Moreover, magnetic fields are produced anyway on a scale (eT)-1 by thermal fluctuations of the gauge fields so that it is unclear what is the difference between magnetic fields produced by the Higgs fields equilibration and these more conventional fields. In our opinion, although Vachaspati's argument is basically correct its formulation was probably oversimplified. Indeed, several works showed that in order to reach a complete understanding of this physical effect a more careful study of the dynamics of the phase transition is called for. We shall now review these works starting from the case of a first order phase transition.
The case of a first order EWPT
Before discussing the SU(2) × U(1) case we cannot overlook some important work which was previously done about phase equilibration during bubble collision in the framework of more simple models. In the context of a U(1) Abelian gauge symmetry, Kibble and Vilenkin [152] showed that the process of phase equilibration during bubble collisions give rise to relevant physical effects. The main tool developed by Kibble and Vilenkin to investigate this kind of processes is the, so-called, gauge-invariant phase difference defined by
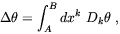
| (4.27) |
where  is the
U(1) Higgs field phase and Dµ
is the
U(1) Higgs field phase and Dµ


 µ
µ
 + e Aµ is the phase covariant
derivative. A and B are points taken in the bubble interiors
and k = 1,2,3.
+ e Aµ is the phase covariant
derivative. A and B are points taken in the bubble interiors
and k = 1,2,3.

 obeys the Klein-Gordon
equation
obeys the Klein-Gordon
equation

| (4.28) |
where m = ev is the gauge boson mass. Kibble and Vilenkin assumed that during the collision the radial mode of the Higgs field is strongly damped so that it rapidly settles to its expectation value v everywhere. One can choose a frame of reference in which the bubbles are nucleated simultaneously with centers at (t, x, y, z) = (0,0,0, ± Rc). In this frame, the bubbles have equal initial radius Ri = R0. Their first collision occurs at (tc, 0, 0, 0) when their radii are Rc and tc = sqrt[Rc2 - R02]. Given the symmetry of the problem about the axis joining the nucleation centers (z-axis), the most natural gauge is the axial gauge. In this gauge
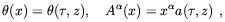
| (4.29) |
where  = 0, 1, 2 and
= 0, 1, 2 and
 2 =
t2 - x2 - y2 .
The condition
2 =
t2 - x2 - y2 .
The condition  a(
a( ,
0) = 0 fixes the gauge completely.
At the point of first contact z = 0,
,
0) = 0 fixes the gauge completely.
At the point of first contact z = 0,
 = tc the
Higgs field phase was assumed to change from
= tc the
Higgs field phase was assumed to change from
 0 to
-
0 to
- 0 going
from a bubble into the other. This constitutes the initial
condition of the problem. The following evolution of
0 going
from a bubble into the other. This constitutes the initial
condition of the problem. The following evolution of
 is determined by the
Maxwell equation
is determined by the
Maxwell equation
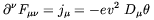
| (4.30) |
and the Klein-Gordon equation which splits into
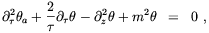
| (4.31) |
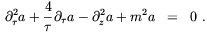
| (4.32) |
The solution of the linearized equations (4.31) and
(4.32) for  >
tc then becomes
>
tc then becomes
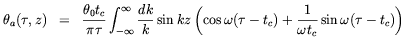
| (4.33) |

| (4.34) |
where  2 =
k2+m2. The gauge-invariant phase
difference is deduced by the asymptotic behavior at z
2 =
k2+m2. The gauge-invariant phase
difference is deduced by the asymptotic behavior at z
 ±
±

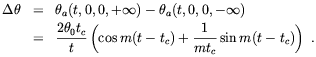
| (4.35) |
Thus, phase equilibration occurs with a time scale tc
determined by the bubble size, with superimposed oscillations with
frequency given by the gauge-field mass. As we see from
Eq. (4.34) phase oscillations come together with
oscillations of the gauge field. It follows from
Eq. (4.30) that these oscillations give rise to an
"electric" current. This current will source an
"electromagnetic" field strength
Fµ (16). Because of the symmetry
of the problem the only nonvanishing component of
Fµ
(16). Because of the symmetry
of the problem the only nonvanishing component of
Fµ is
is
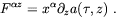
| (4.36) |
Therefore, we have an azimuthal magnetic field
B = F z
= F z =
=

 z a and
a longitudinal electric
field Ez = F0z =
-t
z a and
a longitudinal electric
field Ez = F0z =
-t z
a = -(t /
z
a = -(t /
 )
B
)
B (
( , z),
where we have used cylindrical coordinates
(
, z),
where we have used cylindrical coordinates
( ,
,
 ).
We see that phase equilibration during bubble collision
indeed produces some real physical effects.
).
We see that phase equilibration during bubble collision
indeed produces some real physical effects.
Kibble and Vilenkin did also consider the role of electric
dissipation. They showed that a finite value of the electric
conductivity  gives rise
to a damping in the "electric" current which turns into a damping for
the phase equilibration. They found
gives rise
to a damping in the "electric" current which turns into a damping for
the phase equilibration. They found
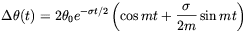
| (4.37) |
for small values of  , and
, and
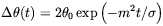
| (4.38) |
in the opposite case. The dissipation time scale is typically much
smaller than the time which is required for two colliding bubble
to merge completely. Therefore the gauge-invariant phase
difference settles rapidly to zero in the overlapping region of
the two bubbles and in its neighborhood. It is interesting to
compute the line integral of
Dk
 over the path ABCD
represented in the Fig. 4.1.
over the path ABCD
represented in the Fig. 4.1.
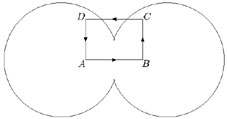
|
Figure 4.1. Two colliding bubbles. It is showed the closed path along which the displacement of the gauge invariant phase difference is computed. (From Ref. [152]). |
From the previous considerations
it follows that 
 AB
= 0,
AB
= 0,

 AD
=
AD
= 
 BC
= 0 and
BC
= 0 and 
 DC
= 2
DC
= 2 0. It
is understood that in order for the integral to be meaningful, the
vacuum expectation value of the Higgs field has to remain nonzero
in the collision region and around it, so that the phase
0. It
is understood that in order for the integral to be meaningful, the
vacuum expectation value of the Higgs field has to remain nonzero
in the collision region and around it, so that the phase
 remains well defined and interpolates smoothly between its values
inside the bubbles. Under these hypothesis we have
remains well defined and interpolates smoothly between its values
inside the bubbles. Under these hypothesis we have
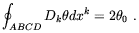
| (4.39) |
The physical meaning of this quantity is recognizable at a glance in
the unitary gauge, in which each

 is given by a
line integral of the vector potential A. We see that the
gauge-invariant phase difference computed along the loop is
nothing but the magnetic flux trough the loop itself
is given by a
line integral of the vector potential A. We see that the
gauge-invariant phase difference computed along the loop is
nothing but the magnetic flux trough the loop itself
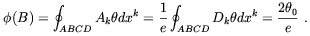
| (4.40) |
In other words, phase equilibration give rise to a ring of
magnetic flux near the circle on which bubble walls intersect. If
the initial phase difference between the two bubbles is
2 ,
the total flux trapped in the ring is exactly one flux quantum,
2
,
the total flux trapped in the ring is exactly one flux quantum,
2 / e.
/ e.
Kibble and Vilenkin did also consider the case in which three
bubbles collide. They argued that in this case the formation of a
string, in which interior symmetry is restored, is possible.
Whether or not this happens is determined by the net phase
variation along a closed path going through the three bubbles. The
string forms if this quantity is larger than
2 . According to
Kibble and Vilenkin strings cannot be produced by two bubble
collisions because, for energetic reasons, the system will tend to
choose the shorter of the two paths between the bubble phases so
that a phase displacement
. According to
Kibble and Vilenkin strings cannot be produced by two bubble
collisions because, for energetic reasons, the system will tend to
choose the shorter of the two paths between the bubble phases so
that a phase displacement  2
2 can never be obtained. This
argument, which was first used by Kibble
[153] for the
study of defect formation, is often called the "geodesic rule".
can never be obtained. This
argument, which was first used by Kibble
[153] for the
study of defect formation, is often called the "geodesic rule".
The work of Kibble and Vilenkin was reconsidered by Copeland and
Saffin [154]
and more recently by Copeland, Saffin and
Törnkvist [155]
who showed that during bubble collision
the dynamics of the radial mode of the Higgs field cannot really
be disregarded. In fact, violent fluctuations in the modulus of
the Higgs field take place and cause symmetries to be restored
locally, allowing the phase to "slip" by an integer multiple of
2 violating the geodesic
rule. Therefore strings, which
carry a magnetic flux, can be produced also by the collision of
only two bubbles. Saffin and Copeland
[156] went a step
further by considering phase equilibration in the SU(2) ×
U(1) case, namely the electroweak case. They showed that for some
particular initial conditions the SU(2) × U(1)
Lagrangian is equivalent to a U(1) Lagrangian so that part of
Kibble and
Vilenkin [152]
considerations can be applied. The
violation of the geodesic rule allows the formation of vortex
configurations of the gauge fields. Saffin and Copeland argued
that these configurations are related to the Nielsen-Olesen
vortices [157].
Indeed, it is know that such a kind of
non-perturbative solutions are allowed by the Weinberg-Salam model
[158]
(for a comprehensive review on electroweak strings see Ref.
[159]).
Although electroweak string are not
topologically stable, numerical simulations performed in
Ref. [156]
show that in presence of small perturbations the
vortices survives on times comparable to the time required for bubble
to merge completely.
violating the geodesic
rule. Therefore strings, which
carry a magnetic flux, can be produced also by the collision of
only two bubbles. Saffin and Copeland
[156] went a step
further by considering phase equilibration in the SU(2) ×
U(1) case, namely the electroweak case. They showed that for some
particular initial conditions the SU(2) × U(1)
Lagrangian is equivalent to a U(1) Lagrangian so that part of
Kibble and
Vilenkin [152]
considerations can be applied. The
violation of the geodesic rule allows the formation of vortex
configurations of the gauge fields. Saffin and Copeland argued
that these configurations are related to the Nielsen-Olesen
vortices [157].
Indeed, it is know that such a kind of
non-perturbative solutions are allowed by the Weinberg-Salam model
[158]
(for a comprehensive review on electroweak strings see Ref.
[159]).
Although electroweak string are not
topologically stable, numerical simulations performed in
Ref. [156]
show that in presence of small perturbations the
vortices survives on times comparable to the time required for bubble
to merge completely.
The generation of magnetic fields in the SU(2) × U(1)Y case was not considered in the work by Saffin and Copeland. This issue was the subject of a following paper by Grasso and Riotto [151]. The authors of Ref. [151] studied the dynamics of the gauge fields starting from the following initial Higgs field configuration
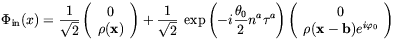
| (4.41) |
which represents the superposition of the Higgs fields of two
bubbles which are separated by a distance b.
In the above na is a unit vector in the SU(2)
isospace and
 a are the Pauli
matrices. The phases and the orientation of
the Higgs field were chosen to be uniform across any single
bubble. It was assumed that Eq. (4.41) holds until the two
bubble collide (t = 0). Since na
a are the Pauli
matrices. The phases and the orientation of
the Higgs field were chosen to be uniform across any single
bubble. It was assumed that Eq. (4.41) holds until the two
bubble collide (t = 0). Since na
 a is the only
Lie-algebra direction which is involved before the collision, one
can write the initial Higgs field configuration in the form
[156]
a is the only
Lie-algebra direction which is involved before the collision, one
can write the initial Higgs field configuration in the form
[156]
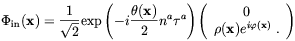
| (4.42) |
In order to disentangle the peculiar role played by the Higgs field phases, the initial gauge fields Wµa and their derivatives were assumed to be zero at t = 0. This condition is of course gauge dependent and should be interpreted as a gauge choice. It is convenient to write the equation of motion for the gauge fields in the adjoint representation. For the SU(2) gauge fields we have
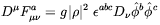
| (4.43) |
where the isovector
 a has been
defined in
Eq. (4.22). Under the assumptions mentioned in the above, at
t = 0, this equation reads
a has been
defined in
Eq. (4.22). Under the assumptions mentioned in the above, at
t = 0, this equation reads

| (4.44) |
In general, the unit isovector
 a can be
decomposed into
a can be
decomposed into
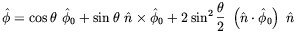
| (4.45) |
where
 T0
T0
 - (0, 0, 1). It is
straightforward to verify that in the unitary gauge,
- (0, 0, 1). It is
straightforward to verify that in the unitary gauge,
 reduces to
reduces to
 0. The
relevant point in Eq. (4.42) is that the
versor [^(n)], about which it is performed the SU(2) gauge
rotation, does not depend on the space coordinates. Therefore,
without loosing generality, we have the freedom to choose
0. The
relevant point in Eq. (4.42) is that the
versor [^(n)], about which it is performed the SU(2) gauge
rotation, does not depend on the space coordinates. Therefore,
without loosing generality, we have the freedom to choose
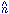 to be everywhere
perpendicular to
to be everywhere
perpendicular to
 0. In
other words,
0. In
other words,  can be
everywhere obtained by
rotating
can be
everywhere obtained by
rotating  0
by an angle
0
by an angle  in the plane
identified by
in the plane
identified by 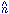 and
and
 0.
Formally,
0.
Formally,  =
cos
=
cos
 0 +
sin
0 +
sin
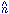 ×
×
 0, which
clearly describes a simple U(1) transformation.
In fact, since it is evident that the condition
0, which
clearly describes a simple U(1) transformation.
In fact, since it is evident that the condition
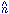

 0 also
implies
0 also
implies 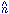

 , the equation of
motion (4.44) becomes
, the equation of
motion (4.44) becomes
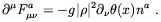
| (4.46) |
As expected, we see that only the gauge field component along the
direction 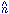 , namely
Aµ = na
Waµ, that has some
initial dynamics which is created by a nonvanishing gradient of
the phase between the two domains. When we generalize this result
to the full SU(2) × U(1)Y gauge
structure, an extra
generator, namely the hypercharge, comes-in. Therefore in this
case is not any more possible to choose an arbitrary direction for
the unit vector
, namely
Aµ = na
Waµ, that has some
initial dynamics which is created by a nonvanishing gradient of
the phase between the two domains. When we generalize this result
to the full SU(2) × U(1)Y gauge
structure, an extra
generator, namely the hypercharge, comes-in. Therefore in this
case is not any more possible to choose an arbitrary direction for
the unit vector 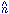 since
different orientations of the unit
vector
since
different orientations of the unit
vector 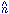 with respect to
with respect to
 0 correspond to
different physical situations. We can still consider the case in
which
0 correspond to
different physical situations. We can still consider the case in
which 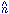 is parallel to
is parallel to
 0 but we
should take in mind that this is not the only possibility. In this case we
have
0 but we
should take in mind that this is not the only possibility. In this case we
have
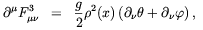
| (4.47) |
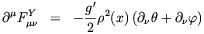
| (4.48) |
where g and g' are respectively the SU(2) and U(1)Y gauge coupling constants. It is noticeable that in this case the charged gauge fields are not excited by the phase gradients at the time when bubble first collide. We can combine Eqs. (4.47) and (4.48) to obtain the equation of motion for the Z-boson field
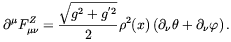
| (4.49) |
This equation tells us that a gradient in the phases of the Higgs
field gives rise to a nontrivial dynamics of the Z-field with an
effective gauge coupling constant sqrt[g2 +
g'2]. We see that the equilibration of the phase
( +
+  ) can be now
treated in analogy to the U(1) toy model studied by Kibble and
Vilenkin [152],
the role of the U(1) "electromagnetic"
field being now played by the Z-field. However, differently from
Ref.
[152]
the authors of Ref.
[151] left the Higgs
field modulus free to change in space. Therefore, the equation of
motion of
) can be now
treated in analogy to the U(1) toy model studied by Kibble and
Vilenkin [152],
the role of the U(1) "electromagnetic"
field being now played by the Z-field. However, differently from
Ref.
[152]
the authors of Ref.
[151] left the Higgs
field modulus free to change in space. Therefore, the equation of
motion of
 (x) has
to be added to (4.49). Assuming the
charged gauge field does not evolve significantly, the complete set
of equations of motion that we can write at finite, though small,
time after the bubbles first contact, is
(x) has
to be added to (4.49). Assuming the
charged gauge field does not evolve significantly, the complete set
of equations of motion that we can write at finite, though small,
time after the bubbles first contact, is
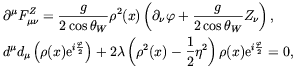
| (4.50) |
where dµ =
 µ
+ i[g / (2cos
µ
+ i[g / (2cos W)] Zµ,
W)] Zµ,
 is the
vacuum expectation value of
is the
vacuum expectation value of  and
and
 is the quartic coupling.
Note that, in analogy with
[152],
a gauge invariant phase difference
can be introduced by making use of the covariant derivative
dµ.
Equations (4.50) are the Nielsen-Olesen equations of
motion [157].
Their solution describes a Z-vortex where
is the quartic coupling.
Note that, in analogy with
[152],
a gauge invariant phase difference
can be introduced by making use of the covariant derivative
dµ.
Equations (4.50) are the Nielsen-Olesen equations of
motion [157].
Their solution describes a Z-vortex where
 = 0 at its
core [160].
The geometry of the problem
implies that the vortex is closed, forming a ring which axis coincide
with the conjunction of bubble centers. This result provides further support
to the possibility that electroweak strings are produced during the EWPT.
= 0 at its
core [160].
The geometry of the problem
implies that the vortex is closed, forming a ring which axis coincide
with the conjunction of bubble centers. This result provides further support
to the possibility that electroweak strings are produced during the EWPT.
In principle, in order to determine the magnetic field produced during the process that we illustrated in the above, we need a gauge-invariant definition of the electromagnetic field strength in the presence of the non-trivial Higgs background. We know however that such definition is not unique [161]. For example, the authors of Ref. [151] used the definition given in Eq. (4.23) to find that the electric current is
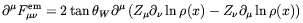
| (4.51) |
whereas other authors [162], using the definition
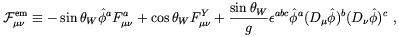
| (4.52) |
found no electric current, hence no magnetic field, at all. We have to observe, however, that the choice between these, as others, gauge invariant definitions is more a matter of taste than physics. Different definitions just give the same name to different combinations of the gauge fields. The important requirement which acceptable definitions of the electromagnetic field have to fulfill is that they have to reproduce the standard definition in the broken phase with a uniform Higgs background. This requirement is fulfilled by both the definitions used in the Refs. [151] and [162]. In our opinion, it is not really meaningful to ask what is the electromagnetic field inside, or very close to, the electroweak strings. The physically relevant question is what are the electromagnetic relics of the electroweak strings once the EWPT is concluded.
One important point to take in mind is that electroweak strings are not topologically stable (see [159] and references therein) and that, for the physical value of the Weinberg angle, they rapidly decay after their formation. Depending on the nature of the decay process two scenarios are possible. According to Vachaspati [163] long strings should decay in short segments of length ~ mW-1. Since the Z-string carry a flux of Z-magnetic flux in its interior

| (4.53) |
and the Z gauge field is a linear superposition of the W3 and Y fields then, when the string terminates, the Y flux cannot terminate because it is a U(1) gauge field and the Y magnetic field is divergenceless. Therefore some field must continue even beyond the end of the string. This has to be the massless field of the theory, that is, the electromagnetic field. In some sense, a finite segment of Z-string terminates on magnetic monopoles [158]. The magnetic flux emanating from a monopole is:

| (4.54) |
This flux may remain frozen-in the surrounding plasma and become a seed for cosmological magnetic fields.
Another possibility is that Z-strings decay by the formation of a W-condensate in their cores. In fact, it was showed by Perkins [164] that while electroweak symmetry restoration in the core of the string reduces mW, the magnetic field via its coupling to the anomalous magnetic moment of the W-field, causes, for eB > mW2, the formation of a condensate of the W-fields. Such a process is based on the Ambj orn-Olesen instability which will be discussed in some detail in the Chap.5 of this review. As noted in [151] the presence of an inhomogeneous W-condensate produced by string decay gives rise to electric currents which may sustain magnetic fields even after the Z string has disappeared. The formation of a W-condensate by strong magnetic fields at the EWPT time, was also considered by Olesen [165].
We can now wonder what is the predicted strength of the magnetic
fields at the end of the EWPT. An attempt to answer to this question
has been done by Ahonen and Enqvist
[166] (see also
Ref. [167])
where the formation of
ring-like magnetic fields in collisions of bubbles of broken phase
in an Abelian Higgs model were inspected. Under the assumption
that magnetic fields are generated by a process that resembles the
Kibble and Vilenkin
[152]
mechanism, it was concluded that
a magnetic field of the order of B
 2 ×
1020 G
with a coherence length of about 102 GeV-1 may be
originated. Assuming turbulent enhancement the authors of
Ref. [166]
of the field by inverse cascade
[51],
a root-mean-square value of the magnetic field Brms
2 ×
1020 G
with a coherence length of about 102 GeV-1 may be
originated. Assuming turbulent enhancement the authors of
Ref. [166]
of the field by inverse cascade
[51],
a root-mean-square value of the magnetic field Brms
 10-21 G on a
comoving scale of 10 Mpc might be
present today. Although our previous considerations give some
partial support to the scenario advocated in
[166] we
have to stress, however, that only in some restricted cases it is
possible to reduce the dynamics of the system to the dynamics of a
simple U(1) Abelian group. Furthermore, once Z-vortices are
formed the non-Abelian nature of the electroweak theory shows due
to the back-reaction of the magnetic field on the charged gauge
bosons and it is not evident that the same numerical values
obtained in
[166]
will be obtained in the case of the EWPT.
10-21 G on a
comoving scale of 10 Mpc might be
present today. Although our previous considerations give some
partial support to the scenario advocated in
[166] we
have to stress, however, that only in some restricted cases it is
possible to reduce the dynamics of the system to the dynamics of a
simple U(1) Abelian group. Furthermore, once Z-vortices are
formed the non-Abelian nature of the electroweak theory shows due
to the back-reaction of the magnetic field on the charged gauge
bosons and it is not evident that the same numerical values
obtained in
[166]
will be obtained in the case of the EWPT.
However the most serious problem with the kind of scenario discussed in this section comes form the fact that, within the framework of the standard model, a first order EWPT seems to be incompatible with the Higgs mass experimental lower limit [143]. Although some parameter choice of the minimal supersymmetric standard model (MSSM) may still allow a first order transition [144], which may give rise to magnetic fields in a way similar to that discussed in the above, we think it is worthwhile to keep an open mind and consider what may happen in the case of a second order transition or even in the case of a cross over.
The case of a second order EWPT
As we discussed in the first part of this section, magnetic fields generation by Higgs field equilibration share several common aspects with the formation of topological defects in the early Universe. This analogy holds, and it is even more evident, in the case of a second order transition. The theory of defect formation during a second order phase transition was developed in a seminal paper by Kibble [153]. We shortly review some relevant aspects of the Kibble mechanism. We start from the Universe being in the unbroken phase of a given symmetry group G. As the Universe cools and approach the critical temperature Tc protodomains are formed by thermal fluctuations where the vacuum is in one of the degenerate, classically equivalent, broken symmetry vacuum states. Let M be the manifold of the broken symmetry degenerate vacua. The protodomains size is determined by the Higgs field correlation function. Protodomains become stable to thermal fluctuations when their free energy becomes larger than the temperature. The temperature at which this happens is usually named Ginsburg temperature TG. Below TG stable domains are formed which, in the case of a topologically nontrivial manifold M, give rise to defect production. Rather, if M is topologically trivial, phase equilibration will continue until the Higgs field is uniform everywhere. This is the case of the Weinberg-Salam model, as well as of its minimal supersymmetrical extension.
Higgs phase equilibration, which occurs when stable domains merge, gives rise to magnetic fields in a way similar to that described by Vachaspati [106] (see the beginning of this section). One should keep in mind, however, that as a matter of principle, the domain size, which determine the Higgs field gradient, is different from the correlation length at the critical temperature [151]. At the time when stable domains form, their size is given by the correlation length in the broken phase at the Ginsburg temperature. This temperature was computed, in the case of the EWPT, by the authors of Ref. [151] by comparing the expansion rate of the Universe with the nucleation rate per unit volume of sub-critical bubbles of symmetric phase (with size equal to the correlation length in the broken phase) given by
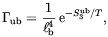
| (4.55) |
where lb is the correlation length in the broken phase. S3ub is the high temperature limit of the Euclidean action (see e.g. Ref. [168]). It was shown that for the EWPT the Ginsburg temperature is very close to the critical temperature, TG = Tc within a few percent. The corresponding size of a broken phase domain is determined by the correlation length in the broken phase at T = TG
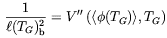
| (4.56) |
where V( , T)
is the effective Higgs potential.
, T)
is the effective Higgs potential.
 (TG)2b is weakly
dependent on MH,
(TG)2b is weakly
dependent on MH,
 b(TG)
b(TG)
 11/
TG for MH = 100 GeV and
11/
TG for MH = 100 GeV and
 b(TG)
b(TG)
 10 /
TG for MH = 200 GeV. Using this
result and
Eq. (4.23) the authors of Ref.
[151] estimated the
magnetic field strength at the end of the EWPT to be of order of
10 /
TG for MH = 200 GeV. Using this
result and
Eq. (4.23) the authors of Ref.
[151] estimated the
magnetic field strength at the end of the EWPT to be of order of
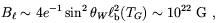
| (4.57) |
on a length scale
 b(TG).
b(TG).
Although it was showed by Martin and Davis
[169] that
magnetic fields produced on such a scale may be stable against thermal
fluctuations, it is clear that magnetic fields of phenomenological interest
live on scales much larger than
 b(TG). Therefore,
some kind of average is required. We are ready to return to the
discussion of the Vachaspati mechanism for magnetic field generation
[106].
Let us suppose we are interested in the magnetic field
on a scale L = N
b(TG). Therefore,
some kind of average is required. We are ready to return to the
discussion of the Vachaspati mechanism for magnetic field generation
[106].
Let us suppose we are interested in the magnetic field
on a scale L = N
 . Vachaspati argued that,
since the Higgs field is uncorrelated on scales larger than
. Vachaspati argued that,
since the Higgs field is uncorrelated on scales larger than
 , its gradient
executes a random walk as we move along a line crossing N
domains. Therefore, the average of the gradient
Dµ
, its gradient
executes a random walk as we move along a line crossing N
domains. Therefore, the average of the gradient
Dµ  over this path should scale as
over this path should scale as
 N. Since the
magnetic field is proportional
to the product of two covariant derivatives, see Eq. (4.23),
Vachaspati concluded that it scales as 1 / N. This conclusion,
however, overlooks the difference between <Dµ
N. Since the
magnetic field is proportional
to the product of two covariant derivatives, see Eq. (4.23),
Vachaspati concluded that it scales as 1 / N. This conclusion,
however, overlooks the difference between <Dµ
 †>
<Dµ
†>
<Dµ
 ;> and
<Dµ
;> and
<Dµ
 †
Dµ
†
Dµ
 >. This point was
noticed by Enqvist and Olesen
[107]
(see also Ref.
[109])
who produced a different estimate for the average magnetic field,
<B>rms, L
>. This point was
noticed by Enqvist and Olesen
[107]
(see also Ref.
[109])
who produced a different estimate for the average magnetic field,
<B>rms, L
 B(L) ~
B
B(L) ~
B /
/  N. Neglecting the
possible
role of the magnetic helicity (see the next section) and of
possible related effects, e.g. inverse cascade, and using
Eq. (4.57), the line-averaged field today on a scale L ~ 1 Mpc
(N ~ 1025) is found to be of the order
B0(1 Mpc) ~ 10-21 G.
N. Neglecting the
possible
role of the magnetic helicity (see the next section) and of
possible related effects, e.g. inverse cascade, and using
Eq. (4.57), the line-averaged field today on a scale L ~ 1 Mpc
(N ~ 1025) is found to be of the order
B0(1 Mpc) ~ 10-21 G.
Another important point of this kind of scenario (for the reasons
which will become clear in the next section) is
that it naturally gives rise to a nonvanishing vorticity. This
point can be understood by the analogy with the process which lead
to the formation of superfluid circulation in a Bose-Einstein
fluid which is rapidly taken below the critical point by a
pressure quench [170].
Consider a circular closed path
through the superfluid of length C =
2 R. This path will
cross N
R. This path will
cross N  C /
C /  domains, where
domains, where
 is the
characteristic size of a single domain. Assuming that the phase
is the
characteristic size of a single domain. Assuming that the phase
 of the condensate wave
function is uncorrelated in each
of the N domains (random-walk hypothesis) the typical mismatch
of
of the condensate wave
function is uncorrelated in each
of the N domains (random-walk hypothesis) the typical mismatch
of  is given by:
is given by:
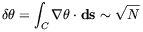
| (4.58) |
where 
 is the phase gradient
across two adjacent domains and ds is the line element
along the circumference. It is well known (see e.g.
[171])
that from the Schrödinger equation it follows
that the velocity of a superfluid is given by the gradient of the
phase trough the relation vs =
(
is the phase gradient
across two adjacent domains and ds is the line element
along the circumference. It is well known (see e.g.
[171])
that from the Schrödinger equation it follows
that the velocity of a superfluid is given by the gradient of the
phase trough the relation vs =
( / m)
/ m) 
 , therefore
(4.58) implies
, therefore
(4.58) implies
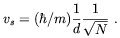
| (4.59) |
It was argued by Zurek [170] that this phenomenon can effectively simulate the formation of defects in the early Universe. As we discussed in the previous section, although the standard model does not allows topological defects, embedded defects, namely electroweak strings, may be produced through a similar mechanism. Indeed a close analogy was showed to exist [172] between the EWPT and the 3He superfluid transition where formation of vortices is experimentally observed. This hypothesis received further support by some recent lattice simulations which showed evidence for the formation of a cluster of Z-strings just above the cross-over temperature [173] in the case of a 3D SU(2) Higgs model. Electroweak strings should lead to the generation of magnetic fields in the same way we discussed in the case of a first order EWPT. Unfortunately, to estimate the strength of the magnetic field produced by this mechanism requires the knowledge of the string density and net helicity which, so far, are rather unknown quantities.
15 Vachaspati
[106]
did also consider Higgs field gradients
produced by the presence of the cosmological horizon. However,
since the Hubble radius at the EWPT is of the order of 1 cm
whereas  ~
(eTc)-1 ~ 10-16 cm, it is easy
to realize that magnetic fields possibly produced by the presence of the
cosmological horizon are phenomenologically irrelevant.
Back.
~
(eTc)-1 ~ 10-16 cm, it is easy
to realize that magnetic fields possibly produced by the presence of the
cosmological horizon are phenomenologically irrelevant.
Back.
16 It is
understood that since the toy model considered by Kibble e
Vilenkin is not SU(2) × U(1)Y,
Fµ is
not the physical electromagnetic field strength.
Back.
is
not the physical electromagnetic field strength.
Back.