Annu. Rev. Astron. Astrophys. 1988. 26: 245-294 Copyright © 1988 by Annual Reviews. All rights reserved

2.2. Indications From Distant Objects

The galaxy redshift surveys described in Section 2.1 extend to z ~ 0.1, Abell rich clusters of distance classes D 4 extend to z ~ 0.1, the more distant Abell clusters extend to z ~ 0.3, quasars extend to z ~ 4, and the cosmic blackbody radiation is believed to have originated at z ~ 1000. These tracers with different limiting effective redshifts facilitate comparison of present large-scale structure with that at epochs extending into the past up to the epoch of hydrogen recombination following the primordial fireball (48, p. 371).

2.2.1. ABELL CLUSTERS     Previous reviews of this topic include Bahcall (11, 13) and Oort (128, pp. 403-8, 417-18).

In 1961, Abell (5) detected superclusters by visual inspection of the surface distribution of rich clusters of galaxies listed in his catalog (4). A rudimentary 1976 study of superclustering among Abell clusters (154, 155) [which examined, for example, the three-dimensional spatial configuration of the 27 Abell clusters of distance classes D 2 (complete sample) with known redshifts from Peterson (146)] was superseded by a parallel, but more extensive and more technically sophisticated 1982-86 analysis by N. Bahcall, R. Soneira, and W. Burgett [which examined, for example, the locational properties of the 104 Abell clusters of distance classes D 4 (statistical sample) with redshifts from Hoessel et al. (90a)]. The Bahcall et al. study confirms the existence of superclusters of Abell clusters and provides a list of their membership (18). [Locations and other properties of the superclusters in the Northern Hemisphere are illustrated in Figure 21 of Oort (128, p. 406); similar but not identical memberships are depicted by the complete-linkage dendrogram, an especially informative branching diagrammatic representation of locational interrelations of Abell clusters (cf. 158 and Figure 7).] The Bahcall et al. study demonstrates that the correlation scale length (cf. Section 3.1.2) of the two-point correlation function of Abell clusters is ~ 50 Mpc, i.e. five times larger than that for galaxies (17) [cf. (65, 148) for evidence from independent observational studies that directly supports this result, and cf. (12, 25, 50, 100) for studies that explain the result astrophysically]. Furthermore, the study shows that if the separation vectors of cluster pairs in superclusters are derived by assuming that observed redshifts can be converted directly into distances through the Hubble relation, then the average radial (i.e. line-of-sight) component of the centroid of a pair, <R>, tends to be larger than the average transverse component, <T> (19). This result is illustrated in Figure 8 with reference to the dendrogram superclusters depicted in Figure 7, and it is most naturally understandable as an effect of a characteristic non-Hubble relative velocity of clusters within superclusters, V ~ 2000 km s^-1. This value significantly exceeds the 600 km s^-1 motion of the Local Group indicated by the anisotropy of the 2.75-K cosmic blackbody radiation and causes serious problems for various cosmological models advanced to explain large-scale structure (cf. Section 3.2.2); therefore, explanations in terms of observational uncertainties and elongation of large-scale structures are also being scrutinized in extensive detail (19). Finally, the Bahcall et al. study demonstrates that superclusters lie on the periphery of the Boötes void (16) [e.g. the Hercules supercluster lies on the near side and the Corona Borealis supercluster lies on the far side (the reader is referred to Figures 4, 5, and 6 for general locational orientation)]; that a void may be present in the three-dimensional distribution of Abell clusters, which extends from l^ll 140° to 240°, b^ll 30° to 50°, z 0.03 to 0.08, and has a characteristic length of ~ 300 Mpc (15); and that the superclusters may be correlated on a scale of ~ 200 Mpc, suggesting the possible existence of the largest structures yet detected (14).

Batuski & Burns (24) and Burns & Batuski (33b) adopt a different approach to the study of large-scale structure with data for Abell clusters. Instead of concentrating on the Abell clusters of the statistical sample with measured redshifts, they apply data for all 2712 Abell clusters (statistical plus nonstatistical sample) with measured plus estimated redshifts. This causes a loss of homogeneity and accuracy in the data base, which, however, is counterbalanced by an increase in the number of tracers that characterize the large-scale structure. Each assigned redshift has been either measured directly or estimated through a calibration curve from the apparent red magnitude of the tenth most luminous cluster galaxy measured by Abell (4). Because the fractional uncertainty of an estimated redshift is _z / z 0.3, the increased sample with estimated redshifts typically causes a decrease of the ratio of signal to noise (S/N) for the identification and delineation of structures, but for very large structures, S/N increases. From the rough three-dimensional distribution of the 652 Abell clusters with measured or estimated redshifts z 0.13, Batuski & Burns (24) constructed a finding list of 102 candidate superclusters and 29 candidate voids with measured or estimated redshifts less than z 0.1. They identified the candidate superclusters as the islands created by the linking of overlapping spheres of sweeping radius R_s = 60 Mpc attached to each Abell cluster. ⁽¹⁾ The four candidate superclusters with the largest membership of Abell clusters and with more than 50% of their redshifts measured are illustrated in Figure 9. Batuski & Burns (23) found that the Pisces-Cetus supercluster (A in Figure 9) located near the southern Galactic cap is part of a possible filament of galaxies and galaxy clusters with a characteristic length ~ 450 Mpc. In an independent investigation (204, 204a), Tully pointed out that if the Supercluster-identifying sweeping radius in the Batuski & Burns sample of Abell clusters is increased by only 50% to R_s = 90 Mpc, then a dramatic change occurs in which the Pisces-Cetus supercluster links with both the Coma/A1367 supercluster and the Local Supercluster. (The linked structure is a band containing ~ 60 rich clusters that stretches across the entire sky through both the southern and northern Galactic caps!) Moreover, the main plane of this Pisces-Cetus supercluster complex (characteristic length ~ 500 Mpc and thickness ~ 60 Mpc) is coincident with the principal plane of the Local Supercluster [characteristic length ~ 50 Mpc and thickness ~ 8 Mpc; cf. (203), (204), and Oort (128, pp. 380-84)], which suggests that the two structures are physically connected. M. Postman, D. Spergel, & B. Sutin (private communication, 1987) are comparing the observational data with corresponding data generated from computer simulations of models that incorporate selection functions derived from the observational data; the results of these comparisons could provide quantitative estimates of the statistical significance of Tully's observational results. A historical precedent for these kinds of studies on the Pisces-Cetus supercluster complex is found in earlier published studies on the Local Supercluster itself (cf. 9, 58, 59).

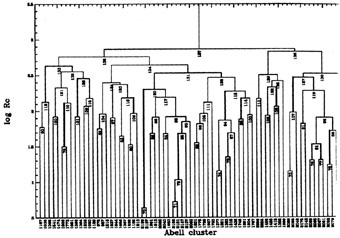
Figure 7. A complete-linkage dendrogram for the statistical sample distance classes D 4 in the northern Galactic hemisphere (cf. 158). The ordinate specifies the similarity level (defined as the logarithm (base 10) of the complete-linkage distance] of a dendrogram supercluster, and the abscissa specifies the Abell designations (4) of its member clusters. Each dendrogram supercluster is represented by a hoop with a similarity bar, below which is written its identification number. (The superclusters Coma/A1367, Hercules/A2199, and Corona Borealis are Nos. 83, 120, and 86, respectively.) The similarity level of this bar represents the diameter of the dendrogram supercluster. The vertical line that extends upward from the center of the bar of the dendrogram supercluster is one of the two branches of the hoop representing the next higher dendrogram supercluster in its membership hierarchy (its neighborhood supercluster). A darkened branch means that the dendrogram supercluster is a physical supercluster modulo L > 20, where L is the local density contrast, i.e. the number density of the dendrogram supercluster divided by the number density of the neighborhood supercluster.

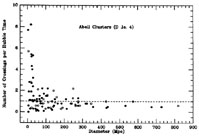
Figure 8. The ordinate represents Ncrossings, the number of crossing distances traversed by a cluster in its dendrogram supercluster over one Hubble time-scale (H0-1). Superclusters in the northern and southern Galactic hemisphere are represented by closed and open circles, respectively. The crossing distance is defined as the radius of a dendrogram supercluster. Ncrossings is estimated from the formula Ncrossings = 2 R / T, where the separation vectors of the Rij-pairs of clusters in a supercluster are estimated from the angular separations and the Hubble distances of the clusters (cz/H0), R is the standard deviation of the radial (i.e. line-of-sight) component of the separation vectors relative to the average for the system, and T is the corresponding standard deviation of the transverse (i.e. in the plane of the sky) component. The abscissa represents Dc, the diameter of a dendrogram supercluster (estimated to be its complete-linkage distance). An interesting exercise for the reader is to identify the selection effect that causes the calculated Ncrossings to approach 0 as Dc approaches the effective limiting diameter of the volume containing the sample of Abell clusters. This figure illustrates (in a different way) the redshift broadening that could indicate the relative velocities of Abell clusters in superclusters of ~ 2000 km s-1 discovered by Bahcall et al. (19).

Although a definitive answer concerning the physical existence of the Pisces-Cetus supercluster complex must await results of quantitative simulation analyses such as that by M. Postman et al. and observational analyses with measured redshifts for the complete sample of Abell clusters with z 0.13, I suggest that the hypothesis of a physically real Pisces-Cetus supercluster complex might make more understandable at least two astronomical puzzles: (a) The polar Galactic extinction derived from the classical interpretation of galaxy counts is much larger than the accepted value (0.2 mag) derived from less suspect methods (59b). The Pisces-Cetus supercluster complex would introduce a previously unrecognized bias that acts in the direction of the effect. The steep selection function in Galactic latitude that has been derived from the surface distribution of Abell clusters (17) (corresponding to an equivalent polar extinction of 0.5 mag) may also contain a component from this very large structure. The discovery by Kirshner et al. (104) that the galaxy distribution is significantly smoother in a sampling of the south Galactic polar cap than in a sampling of the north Galactic polar cap may be related to the structure of the Pisces-Cetus supercluster complex. (b) The Local Group moves with a velocity of 600 km s^-1 relative to the frame of the cosmic microwave background (212a), which is consistent (within the uncertainties of measurements of velocities and especially distances) with results from local samples of galaxies within an effective distance of ~ 100 Mpc (2, 6, 50a, 113b). There is also an indication from studies of kinematic properties of elliptical galaxies within a distance of ~ 100 Mpc that this entire local region might be participating in this motion (6, 113b). Bulk motion would be understandable if the Pisces-Cetus supercluster exists, and part or all of the 600 km s^-1 motion of the Local Group relative to the frame of the microwave background could be caused by the gravitational attraction of this supercluster complex. [A local feature sometimes called the "Great Attractor," located at a distance of ~ 90 Mpc positioned on the sky just below the Centaurus cluster (Figure 10), has previously been suggested to cause bulk streaming motion (6, 113b). Comparison of Figures 8 and 9 indicates that the "Great Attractor" is located on the great circle of the Pisces-Cetus supercluster complex and hence is likely to be a nearby part of this relatively planar structure.] The mass of the Pisces-Cetus supercluster complex is M = 10¹⁷ - 10¹⁸ M, derived by Tully (204) from summing the mass expected to be associated with the number of Abell clusters in the complex (cf. 12, 45) and, alternatively, by estimating the fraction of mass in the volume occupied by the complex in a universe with a density parameter 0.1 < < 1. The Local Group and the galaxies in its environs would be falling toward the center of the Pisces-Cetus supercluster complex with an infall velocity given by V_in = GM / R²H₀. For R ~ 250 Mpc and M ~ 10¹⁷ - 10¹⁸ M, v_in ~ 150-1500 km s^-1, consistent with the observed peculiar velocities relative to the Hubble flow (e.g. V_in = 600 km s^-1 corresponds to M 4 × 10¹⁷ M).

The location of the ~ 300 Mpc void identified by Bahcall & Soneira (15) (see above) is noted in the caption for Figure 9. From analysis of their extended sample of Abell clusters, Batuski & Burns (24) and D.J. Batuski et al. (private communication, 1987) find that this is indeed an extremely large region of very low cluster density: knowledge of whether or not it will break up into a collection of smaller voids, however, must await direct redshift measurements for the Abell clusters whose estimated redshifts would place them in or near this void.

Figure 9. Aitoff equal-area projection of the celestial sphere in Galactic latitude (bll) and longitude (lll) displaying the locations of the Abell clusters in all richness classes (R = 0-6) contained in four of the supercluster candidates of Batuski & Burns (24). Octagons and triangles signify clusters with measured redshifts and estimated redshifts, respectively. The legend contains the limits of the sizing scheme for the symbols (linear in redshift). The four candidates, outlined by contour lines, are (A) Pisces-Cetus, (B) Sextans-Leo, (C) extended Hercules, and (D) Aquarius. By inspecting the chart representing the sky distribution of Abell clusters reproduced in Figure 20 of Oort (128, p. 404), we note that the zone of Galactic obscuration lies between bll - 30°, and bll 30° and that the southern equatorial hemisphere, which (for practical reasons) is not part of the Palomar Observatory Sky Survey, lies primarily in the lower right-hand quadrant of the plot. The region occupied by the Pisces-Cetus supercluster complex, with its characteristic length ~ 500 Mpc studied by Tully (204), extends from the elongated Pisces-Cetus superclustcr (A) through the Galactic plane at lll ~ 120° and the Coma cluster near the northern Galactic pole. The Local Supercluster (centered near lll = 284°, bll = 74°) is contained within this supercluster complex. The void of Abell clusters, with its characteristic length ~ 300 Mpc identified by Bahcall & Soneira (15), extends from lll 140° to 240°, bll 30° to 50°, and redshift z 0.03 to 0.08. Reproduced from (24) by permission of D.J. Batuski and J.O. Burns.

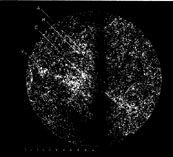
Figure 10. Computer-generated sky map by O. Lahav of galaxies with blue magnitude smaller than mp ~ 14.5. The plot is centered at lll = 307 , bll = 9, the direction of streaming motion found from a sample of elliptical galaxies within a volume of radius 100 Mpc by Lynden-Bell et al. (113b). The dark vertical band represents the zone of avoidance caused by Galactic obscuration. The location of the Galactic center is 37 up from the bottom of the picture. The Virgo (V), Centaurus (C), Hydra (H). and Antilia (A) clusters are indicated. The "Great Attractor" is the great concentration of galaxies just below the Centaurus cluster. The nonlinear scale indicates 9 intervals spanning the range from the center to the edge of the picture. Reproduced from (113b) by permission of Sandra Faber and O. Lahav.

¹ This "percolation technique" introduced in another context by Turner & Gott (205a) and later introduced to the study of superclustering by Zel'dovich et al. (216) is discussed more fully by Oort (128 pp. 409-11), and is one of a family of related supercluster identification techniques (Section 3.1.3). A given sweeping radius applied to a sample of clusters that is selection-free (or for which selection effects have been removed) specifies a given minimum local number density for supercluster membership, _min = (4 R_s³ / 3)^-3. which corresponds to a minimum global density contrast _G; for example, Bahcall & Soneira (18) identified 16 superclusters with _G 20. Back.