Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

2.2. The Idea of Geometrical Experiments

How then are we to measure deviations from Euclidean predictions? What rules concerning the properties of measuring rods do we adopt, and by what rules do we assess whether an experiment has given a non-Euclidean result? Early on, Poincaré denied the reality of actual curved space by stating that in any measurement that appeared to give a non-Euclidean result, one is at liberty to redefine the properties of the measuring rods in such a way as to recover a Euclidean prediction. A particularly interesting example of this, involving nonuniformly heated metal measuring rods, is given by Robertson (1949). Poincaré's point has been variously debated (cf. Whittaker 1958, Reichenbach 1958) with the consensus opinion being that contrived (unreasonable) explanations of changes in the measuring rods, if they are required to save the Euclidean case, are less desirable than a real Riemann-Lobachevski geometry. The debate then changes to the meaning of contrived and unreasonable. Consider again the Fitzgerald contraction of fast-moving measuring rods, and ultimately the reality of the Lorentz transformation. The issue is now resolved in Einstein's (1905) favor in that his deeper interpretation of space-time is viewed as more reasonable than the Fitzgerald explanation, which is now viewed as contrived.

In cosmology we are faced with similar problems. We cannot measure distances by placing rigid rods end to end. Rather, operational definitions of distance "by angular size," "by apparent luminosity," "by light travel time," or "by redshift" are perforce employed. Their use then requires a theory that connects the observables (luminosity, redshift, angular size) with the various notions of distances (McVittie 1974). One of the great initial surprises is that these distances differ from one another at large redshift, yet all have clear operational definitions. Which distance is "correct?" All are correct, of course, each consistent with their definition. Clearly, then, distance is a construct in the sense of Margenau (1950), operationally defined entirely by its method of measurement.

The best that astronomers can do is to connect the observables by a theory and test predictions of that theory when the equations are written in terms of the observables alone. To this end, the concept of distance becomes of heuristic value only. It is simply an auxiliary parameter that must drop from the final predictive equations.

But spatial curvature appears on a different footing. Although it too cannot be directly measured without a covering theory of "luminosity distance" or "redshift distance" to relate "volumes" to "distance," the curvature does enter as a primary parameter (not to be dropped from the equations) in the predictive relations between the observables (luminosity, angular diameter, and redshift). The curvature is

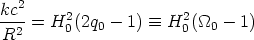
(1)

if = 0. The parameter q₀ (or ₀) enters into all the equations connecting redshift, luminosity, angular size, and number counts. In this sense, the curvature is measurable and therefore is "real," because it has observable effects on the m(z), (z), and N(z) relations.

Direct experimental geometry is then a possibility, provided that we are willing to accept the equations that connect the q₀ measure of curvature with angles, areas, volumes, and redshifts - equations derived from some adopted cosmology.