Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

2.3. Line Lengths and Areas on a Sphere of Constant Curvature

Experimental geometry can be illustrated by showing how the radius (of curvature) of a sphere can be found by measurements of line lengths, areas, and angles made entirely on its surface. The curvature K = 1/R₁R₂ is the product of the reciprocals of the radii of the two osculating circles to the geodesics drawn on the surface at any particular point P, put in the directions of maximum and minimum descent. Examples of surfaces of constant curvature are the sphere (where K is positive) and the pseudo-sphere (where K is negative).

Consider the experimental determination of the radius R (i.e. K^-1/2) of a sphere found by measuring lengths, areas, or angles on its surface. From any point P on the surface, proceed a distance r from P and draw a circle about P of radius r (along the surface). The length of this circle is

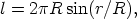
(2)

which for r small compared with R is, to second order,

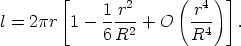
(3)

This differs from 2r for a Euclidean plane (K = 0), permitting a determination of R once l and r are measured on the surface itself!

In a similar way, the areas of a spherical cap drawn about a point P with radius r along the surface is

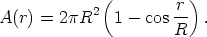
(4)

For small r/R, Equation 4 can be expanded to

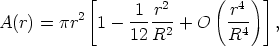
(5)

which again differs from r² for a space of zero curvature.

The deviation from Euclidean geometry is small. At the enormous distance of r = R, along the surface, Equation 4 shows that the area is 0.92r², differing from the Euclidean case by only 8%. This special case illustrates the general proposition that one must sample a very large fraction (i.e. of the order of curvature radius R) of any non-Euclidean space before deviations from the geometry of the Euclidean tangent. space become measurable.

Besides lines and areas, the sum of the angles of triangles placed on the surface also measures the curvature. It can be shown that the difference of the angle sum from 180° for any triangle is the curvature times the area of the triangle, i.e.

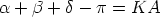
(6)

where , , and are the interior angles of the triangle, and K is the curvature of the surface at the triangle. The special case of a hemisphere illustrates the theorem. The area of the hemisphere is 2R². The sum of the angles of the spherical triangle that forms the hemisphere is 2 + /2 + /2 = 3. The angular excess of 3 - divided by the area is R^-2, which is the curvature K as stated by Equation 6. It can be shown that this equation holds for any surface of constant Gaussian curvature.

Note that Equations 2, 4, and 6, which measure different aspects of the geometry (lines, areas, and angles), all contain the common term R^-2 = K. A case for the reality of space curvature would be strong if the measurements of quite a different nature that are required to test each of the three equations would give the same value of R^-2. In a similar way in cosmology, some confidence in the value of the geometrical parameter q₀, which is related to the curvature via Equation 1, would obtain if multiple experiments of different kinds gave the same result. This congruence of answers is the goal of the observational quest.

Now to the details of the standard model.