Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

3. COUNT-REDSHIFT RELATION

3.1. The Coordinate r as a Function of Redshift

The relation between time and distance for a light ray is given by the null geodesic of the space-time interval whose metric is

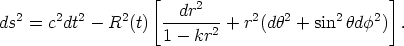
(15)

Orienting the axes so that = = 0 and putting ds = 0 gives the basic equation of the problem as

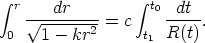
(16)

Using Equation 12, we finally obtain

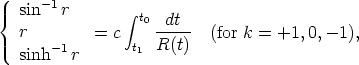
(17)

which if R(t) is a known function of time will give r(t). This is related to the redshift z / ₀ by the Lamaitre Equation

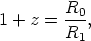
(18)

where R₀ and R₁ are the scale factors at the times of light reception and fight emission, respectively.

The time variation of R is given by the solution of the dynamical Friedmann equation

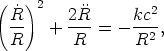
(19)

which is fundamental to the standard model. Integration of this equation gives R(t), which when put in Equation 17 gives the r(z) connection via Equation 18. This in turn, when put in Equations 9-11 gives V(z), which solves the problem in closed form.

Two special cases illustrate the method. Consider first the Euclidean case of k = 0. The well-known solution of Equation 19 for R(t_i) at time t_i is

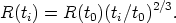
(20)

When this is put into the right side of Equation 17 and integrated, using Equation 18 to relate z with the ratio of the scale factors, we obtain

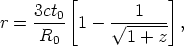
(21)

which, with t₀ = 2/3H₀^-1, where H₀ = / R, gives

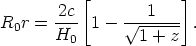
(22)

This, put into Equation 11, gives

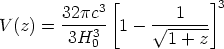
(23)

for the volume enclosed in redshift distance z for the Euclidean case (k = 0).

Consider next an empty universe (no mass). In this case, 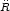= 0, k = - 1, and Equation 19 integrates directly to

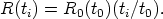
(24)

Equation 24 put into the right side of Equation 17 gives

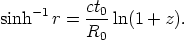
(25)

Noting that t₀ = H₀^-1 in this case, we obtain, after reduction,

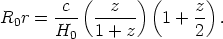
(26)

Using Equation 1, and remembering that q₀ = - 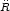/ R₀H₀² = 0 in this case, gives R₀ = c/H₀, hence

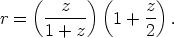
(27)

Equations 26 and 27, substituted into Equation 10, give V(z) for an empty universe explicitly.

We have now introduced the dimensionless deceleration parameter q₀, which is convenient in expressing the general case. This parameter first arose in the literature via series expansions of the relevant observational equations (Heckmann 1942, Robertson 1955, McVittie 1956, Davidson 1959), where no recourse to the solution of the Friedmann equation was needed. Before Mattig's (1958, 1959) exact (closed) solutions were known, Taylor expansions of R(t) were made backward in time starting with the time of observation t₀. This required no knowledge of the Friedmann solution but merely an assumption that R(t) is well enough behaved for a Taylor series to exist. These series expressions for the V(z), m(z), and (z) tests sufficed for small redshifts, but not for redshifts of arbitrarily large size. In contrast, Equations 21, 22, 26, 27 are exact for all values of z. It follows that their use in Equations 9 and 10 for the volumes also apply to any value of the redshift. The reason is that we have used the complete solution for R(t) from Equation 19 in Equation 17 rather than a Taylor series.

The value of q₀ determines the size of the space curvature via Equation 1. This, in turn, is related to the matter density (Hoyle & Sandage 1956) by

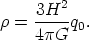
(28)

For any arbitrary value (hence q₀ value) we seek general formulae for r(z) and Rr(z). Equations 21, 22, 26, and 27 are special cases of these formulae. We need the general solution of the Friedmann equation (Equation 19) for any arbitrary value of the curvature kc² / R².

Mattig (1958) shows that this solution is

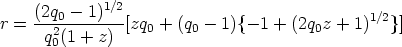
(29)

and

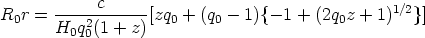
(30)

for all values of q₀. A transparent derivation of these equations in terms of the parametric cycloid and hypercycloid development angle was given by Sandage (1961b).