Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

3.2. The Predicted K(z, q₀) Relation

Combining Equations 9-11 with Equations 29 and 30 gives the exact N(z, q₀) relation, calculated therefrom directly in parametric form. A calculation via this route shows the dependence of N(z) on curvature for three q₀ values in Figure 1. The normalization of the volume is arbitrary in this diagram; N(z) is proportional to V(z), the proportionality factor being the volume density of galaxies.

Figure 1. Theoretical N(z, q0) relations for three values of q0. Plotted is the integral count, i.e. the total number of galaxies in a complete (volume-limited) sample that have redshifts smaller than z. Parts (a) and (b) are the same function but plotted as log z(a) and z(b).

The lowest value of q₀ shown in Figure 1 is that which is required by adding the luminosity density of galaxies obtained from the observed N(m) data. As discussed by Binggeli et al. (1988) in their review of the luminosity function in this volume, this minimum permissible value of q₀ is

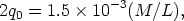
(31)

which is q₀ = 0.03 if M / L = 40. The second case shown in Figure 1 is for ₀ = 1(q₀ = 1/2) required by Grand Unification. The third case (q₀ = 1) is for a highly curved Reimannian space of curvature c² / R² = H₀². If H₀ = 50 km s^-1 Mpc^-1, the radius of curvature would be R = 6000 Mpc, which is only 300 times the distance to the Virgo cluster!

Figure 1a shows N(z, q₀) vs. log z. Figure 1b is the same calculation, but it is displayed in z rather than log z. The marked interval along the ordinate is a actor of 10 in the counts. For small redshifts (z < 0.1) the slope of N(z) curves for all reasonable q₀ is d log N(z)/dz = 3, becoming considerably flatter for higher redshifts, as marked along the curves in Figure 1a. For large redshifts, the volume becomes much smaller than the z³ Euclidean case for q₀ > 1/2, but larger for the hyperbolic geometry of q₀ < 0.5. The ratio of the volumes encompassed from the observer to redshift z for q₀ = 0 compared with q₀ = 0.5 is shown as a function of z in the table in Figure 1a.