Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

4.3. The Predicted Hubble Diagram With Correction for Luminosity Evolution

In an evolving universe, the mean age of galaxies decreases with increasing redshift simply because we sample earlier times as we look out in distance. A first estimate of the expected change of E galaxy luminosities with look-back time, based on the change of the turnoff luminosity in the HR diagram for an old coeval population, gave a mean evolutionary rate of L ~ t^-4/3 for a flat luminosity function at the main sequence turnoff (Sandage 1961b). Because the luminosity function is not flat but rises for faint magnitudes below the turnoff, this is an upper limit, overestimating the luminosity rate by about 30%.

Call the change of magnitude due to evolution E(t). Equation 33, transformed to heterochromatic magnitudes, then becomes

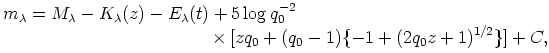
(35)

which is a basic equation that is used extensively in the following sections.

As for the size of E(t), the simple evolution rate for an old coeval population of L ~ t^-4/3 quoted above would give a magnitude variation of mag = - 2.5 log t₀ / t₁, where t₀ and t₁ are the ages of the source at light reception at the Earth and at light emission from the source, respectively. If t₀ = 15 × 10⁹ yr and we inquire for the case of a look-back time of 10⁹ yr, then mag = - 2.5 log(15/14)^4/3 = 0.10 mag for small t₀/t. The sense of the correction is that galaxies were brighter in the past. If this rate is ~ 30% too high (Tinsley & Gunn 1976), the rough estimate of E(t) is then ~ 0.07 mag per 10⁹ yr.

Elaborate calculations of E(t) form the subject of galaxy evolution via stellar population synthesis, pioneered by Tinsley (1968, 1972a, b, 1976, 1977a, b, 1980, and references therein) and her colleagues. The exact rate depends on the various assumptions of star formation rates over time and on the slope of the main sequence luminosity function. However, order-of-magnitude corrections, changing t to z via equations in the next section, give m - 2.5 log(l + z). For small z the correction again is approximately 0.07 mag per 10⁹ yr on a time scale of t₀ ~ 15 × 10⁹ yr for the age of the Universe-nearly the same as the early, quite elementary estimates.

For very large redshifts, where the look-back times are of the order of the age of the Universe, much more elaborate evolutionary models are required than simple main sequence burn-down rates near the present main sequence termination point. The philosophy by which the rates can be calculated near the beginning of galaxy formation was first set out by Tinsley (1968). Modern calculations include those of Bruzual & Kron (1980), Bruzual (1981, 1983a, b), and Arimoto & Yoshii (1986, 1987). A summary of E(t) over the age range of 10⁷ to 1.5 × 10¹⁰ yr is given by Yoshii & Takahara (1988, their Figure 2) for E/S0 and Sdm galaxies in the UBVRIJK photometric bands.