Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

4.4. The Look-Back Time as a Function of A and q₀

To use Equation 35 we must change E(t) into E(z) by the relation between the look-back time = t₀ - t₁ and the redshift as a function of q₀. The general case requires the closed solution of R(t) from the Friedmann equation. Before setting down this general solution, it is instructive to consider again the simple cases of q₀ = 0 and q₀ = 1/2 for empty space and for flat space-time, respectively.

Recall that R(t) ~ t for q₀ = 0 and R(t) ~ t^2/3 for q₀ = 1/2. Using these dependencies and the Lemaitre equation of R₀/R₁ = 1 + z gives the following relations for the look-back time:

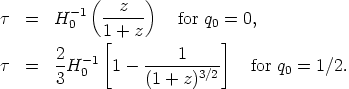
(36)

The general case for any q₀ is found by combining the age equations (Sandage 1961a, Equations 61 and 65) of T₀ = f (q₀, H₀) with the R₀/R₁ = q(z, q₀) Friedmann solution, together with R₀/R₁ = 1 + z. Tables are given in Sandage (1961b).