Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

5.2. The Full Complication of the N(m, q₀, E) Prediction, Given E(z) and the Luminosity Function (M, T)

For the real case we must integrate over the luminosity function. Because this function changes in shape and normalization with galaxy type (Binggeli 1987, Binggeli et al. 1988) and because K(z) in Equation 35 is also a strong function of type, separate integrations are required for each Hubble morphological class. The results for a given type are then summed over all types using an assumed galaxy mix.

The integration over absolute luminosity, and over the sheets and voids of the galaxy distribution, is done by the usual equation of stellar statistics:

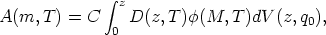
(38)

where A(m, T) is the number of galaxies of type T per unit area at m in interval dm, C is a normalization factor used to convert the absolute density (in number of galaxies of type T per cubic parsec) to units of number of galaxies per unit area, D(z, T) is the density at distance z of type T,(M, T) is the luminosity function read at M in interval dM for galaxies of type T, and dV(z, q₀) is the volume element between redshift z₁ and z₂ corresponding to the magnitude interval between m - dm and m + dm.

The total number of galaxies brighter than m is

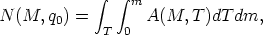
(39)

i.e. A(m, T) summed over type and magnitude.

To apply Equation 38 we must use Equations 9-11, 29, and 30 for V(z, q₀), together with the m(M, z, q₀, E) relation of Equation 35. In this way, all variables in Equation 38 can be related to each other, albeit in a multiparametric way.

The simplest practical method for solving Equation 38 is to replace the integral by a summation over shells bounded by redshifts z₁and z₂, such that the apparent magnitude [for fixed M - K(z) - E(z) values] at z₂ differs by one magnitude from that at z₁. An m, log -like table can then be constructed by the method of Kapteyn (cf. Bok 1931, 1937, Mihalas & Binney 1981). Such a table has cells separated by a unit apparent magnitude interval along the top of each column and by z₁ and z₂ boundaries for the rows. In each (m, z₁ - z₂) cell a particular M - K(z) - E(z) value applies via Equation 35. The volume element in each row, given by Equations 9-11, 29, and 30, can be multiplied by the (M, T) and D(z) that applies to each cell [i.e. at a given <z> = 1/2(z₁ + z₂)]. The sum of each column is the A(m) value for a given type. The process is then repeated for each type, and the A(m) values are summed via Equation 38 to give N(m, q₀).

This, or an equivalent method, has presumably been used by those who compare galaxy counts with predictions of the models, although the methods have not been described in detail in any of the original archive papers in the literature, now to be discussed.