Copyright © 1988 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1988. 26:
561-630 Copyright © 1988 by Annual Reviews. All rights reserved |
9.3. Value of H0
In these pages Hodge (1981) reviewed the debate up to ~ 1980 on the value of the Hubble constant, giving extensive references. Since that time attempts have been made to discover the source of the factor of 2 difference in H0 between the long- and the short- distance scale workers. A factor of 2 in distance at a given redshift is equivalent to 1.5 magnitude (factor of 4 in luminosity). The source of the discrepancy must be sought and convincingly found if the matter is to be put to rest while members of the present generation are still active.
The factor of 2 is not in the local calibrators (Tammann 1987a, b), where at most only ~ 0.3 mag separates the various adopted calibrations. The explanation is almost certainly to be found as bias effects in the analysis of data from flux-limited catalogs, no matter what distance indicator is adopted, if that indicator is anything other than redshift. The proof of this statement is the apparent increase of H0 with redshift, ranging from 50 km s-1 Mpc-1 locally to > 100 at ~ 4 times the Virgo cluster, obtained in all of the analyses by the advocates of the short scale (cf. de Vaucouleurs & Peters 1986, their Figure 2; Giraud 1986a, b, 1987). Discussions of this bias and why the apparent increase of H0 with distance is an artifact include those by Teerikorpi (1975a, b, 1984, 1987), Sandage et al. (1979), Bottinelli et al. (see their 1987 and 1988 papers for a review), Kraan-Korteweg et al. (1986, 1988), and Sandage (1988a, b).
There have been many ways to discuss this type of Malmquist bias in flux-limited samples, most of which are complicated enough to be but dimly understood except, perhaps, by their authors. Figure 15 illustrates still another discussion of the effect and its consequences. Shown is a schematic m(z) Hubble diagram using objects that have a spread in absolute magnitude M. Parallel envelope lines drawn to encompass the sample define the loci of absolute magnitudes M1 and M2. (For a linear velocity-distance relation, recall that the slope of these lines is dm/d log z = 5.) Divide the data into redshift zones, labeled 1-10 and shown hatched in Figure 15. If the sample is taken from a magnitude-limited catalog, there will be a limit line as shown, for which no objects in the sample are fainter. Consider now the mean (ridge) line of the data sample in the z, m plane. The true mean <MT> value is seen in the data up to distance interval 4-5, but beyond that the data begin to be systematically too bright compared with the true value of <MT>.
What are the consequences? Suppose we assign an absolute magnitude <MT> to each galaxy in the sample. For those closer than distance interval 5-6 we will make as many positive as negative errors in the correct m - M distance modulus due to the luminosity spread in M. This part of the sample is distance limited. However, the flux limitation of the fainter sample progressively removes fainter absolute magnitudes from the remaining set as the true distance increases, giving false (biased) mean m - M values. The inferred distances are too small in the mean for this subsample (because the <MT> used is too faint to apply to it, as shown by the position of the crosses). By using these incorrect inferred photometric distances to obtain H0, progressively larger (incorrect) values of H0 would be obtained as an artifact. Note that the correct value of H0 is that obtained only in the distance interval closer than 5-6.
Detailed analysis of actual data
(Sandage 1988a,
b)
has shown this
bias explicitly in samples of ScI galaxies and in galaxies used for
the Tully-Fisher distance scale method. By reading the data in the
redshift limit of
z  0,
low values of H0 have been obtained using the
local calibrators with Cepheid distances. This is equivalent to the
method of
Richter & Huchtmeier
(1984),
who restrict their sample to the distance-limited list of
Kraan-Korteweg &
Tammann (1979)
and obtain a low value of H0 directly (cf.
Sandage 1988b).
0,
low values of H0 have been obtained using the
local calibrators with Cepheid distances. This is equivalent to the
method of
Richter & Huchtmeier
(1984),
who restrict their sample to the distance-limited list of
Kraan-Korteweg &
Tammann (1979)
and obtain a low value of H0 directly (cf.
Sandage 1988b).
From these studies, together with a cluster data analysis with the Tully-Fisher method (Kraan-Korteweg et al. 1988), the value of the Hubble constant has been found to be in the range
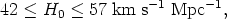
|
where the formal error is adopted to be ~ ± 10% from individual studies. The value found from supernovae of type Ia, using both an empirical (Sandage & Tammann 1982) and a theoretical calibration (Sutherland & Wheeler 1984, Arnett et al. 1985) of the absolute magnitude, gives (Cadonau et al. 1985)
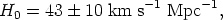
| (56) |
which in turn gives a Hubble time of H0-1 = 22.7 ± 5.5 Gyr.