B. Model of a nebula whose internal viscosity is very great

This model is built up of stars, dust, and gases in such fashion that the gravitational interactions between the various components, as well as direct impacts, influence the path of every component mass in a radical way. Many changes in energy and momentum of every component mass will take place during time intervals that are short compared with the time an unperturbed mass of the same initial velocity would consume to traverse the system.

Conditions of motion in this model are analogous to the conditions of motion of elementary particles in a star. This model of a nebula, therefore, will rotate like a solid body, regardless of what its total mass and the distribution of mass over different regions of the system may be. The conclusion which has sometimes been put forward, ⁽²⁾ that constant angular velocity necessarily implies uniform distribution of mass, is obviously erroneous. Furthermore, it is again seen that the rate of rotation of a stellar system has no very direct bearing on its total mass.

C. Actual nebulae

Good mechanical models of actual nebulae may presumably be constructed by combining the distinctive features of the two limiting cases described in the preceding sections. Such a combined model will possess a central, highly viscous core whose relative dimensions are not negligible but are comparable with the extension of the whole system. If the outlying, and among themselves little interacting, components of the nebula had no connection with the central core, we might, at a given instant, observe average angular velocities which, as a function of the distance r from the center of rotation, would be given by

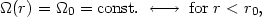
(1)

where r₀ is the radius of the core. For r > r₀, the angular velocity (r) would be essentially arbitrary. In reality, however, the viscosity will not drop abruptly to zero at r = r₀. From an inspection of the distribution of the outlying masses in many nebulae it would seem that these masses at some previous time must have formed part of the central core. They may have been ejected from this core because they acquired high kinetic energy through many close encounters, or they may be the result of a partial disruption of the core by tidal actions caused by encounters with other nebulae (Jeans). At the moment these outlying masses have passed the boundary of the core, their average tangential velocities must have been of the order r_{0 0}. Assuming that these masses in regions r > r₀ are essentially subject only to the gravitational attraction of a central spherical core and that the interactions among themselves may be neglected (the internal viscosity of the outlying system is equal to zero), the average angular velocity (r) outside the core will be approximately given as

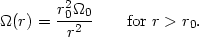
(2)

This relation simply expresses the fact that a mass m which, on being ejected from the core with a tangential velocity v_t relative to this core, describes an orbit whose angular momentum,

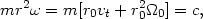
(3)

is a constant. If the average 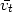for many particles leaving the core is zero, the average angular velocity 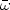= of all the particles in a given point is obtained from

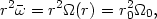
(4)

which is the same as (2). Unfortunately, relation (2) is superficially very similar to the relation obeyed by the angular velocities _c of a system of circular planetary orbits around a heavy central mass M. For such an orbit we have

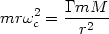
(5)

or

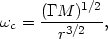
(6)

where is the universal gravitational constant. The similarity of the dependence on r in (2) and (6) will in reality become still greater, since the rate of decrease of (r) with increasing values of r will in actual nebulae be more gradual than that given by (2), owing to the fact that the internal viscosity will not vanish abruptly at r = r₀ but will disappear gradually with increasing r. The observed angular velocities in the outlying regions of nebulae actually show a dependence on r which resembles the relation (6). This relation was, therefore, sometimes erroneously used for the determination of the mass M. The preceding discussion, however, indicates that the observed angular velocities may be adequately accounted for on the basis of the considerations resulting in relation (2) rather than in relation (6). This again shows clearly that it is not possible to derive the masses of nebulae from observed rotations without the use of additional information, since the relation (2) does not contain the mass M at all.