


D. Further discussion of the rotation of nebulae
From the analysis of an appropriate mechanical model of actual nebulae we have derived in the preceding section the following approximate dependence on r of the average tangential velocity Vt:
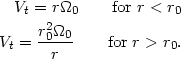
| (7) (8) |
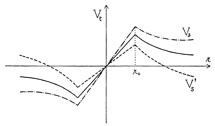
This dependence is pictured in Figure 1. The observed curves Vt(r) are similar to the schematic curve of Figure 1. From this similarity we infer that the cores of nebulae possess considerable internal viscosity. The problem of deducing theoretical values for this viscosity therefore arises. It will be interesting to see whether the gravitational interactions in dense stellar systems are sufficient to account for the fact that such systems rotate like solid bodies, or if it is necessary to introduce matter in the form of dust particles and gases.
|
Figure 1. Velocity of rotation in nebulae |
The point of view adopted in the preceding discussion automatically eliminates the discrepancy which was thought to exist, with respect to the distribution of mass in nebulae as derived from data on internal rotations, on the one side, and from the shape and the distribution of the isophotal contours, on the other. The tremendous increase of surface brightness from the edge, r = r0, of the core of nebulae to their center, r = 0, indicates a correspondingly large increase of mass density. The erroneous idea 2 that the constancy of the angular velocity throughout the core necessitates the assumption of a constant mass density therefore created an apparently insoluble paradox. This paradox, however, disappears as soon as we introduce the idea of an internal gravitational viscosity of stellar systems, which equalizes the angular velocity throughout such systems regardless of the distribution of mass. How this viscosity may be expressed in terms of the gravitational interactions of stars will be discussed in another place.
One further interesting problem presents itself. The distribution of matter in a stellar system which has an internal viscosity as high as we have assumed it to be in the cores of nebulae should rapidly converge toward stationary conditions. The determination of the density distribution in such a system should be analogous to the determination of the density distribution in gravitating gas spheres. R. Emden's analysis (3) of such spheres may, therefore, prove useful in the study of globular and elliptical nebulae as well as in the study of cores of spiral nebulae.
In concluding this section the question may be raised whether data on the internal rotation of nebulae, supplemented by certain additional information, make possible the determination of nebular masses. This question, in principle, must be answered in the affirmative. For instance, data on internal velocities combined with the virial theorem discussed in the next section may ultimately furnish good values for the masses of globular and elliptical nebulae as well as the cores of certain spirals. In the case of open spirals, an investigation of the geometrical structure of the spiral arms, combined with velocity data, promises to be helpful. In this connection a few remarks may be in order regarding the possibility of the formation of spiral arms in our simple mechanical model of nebulae.
Consider the two alternatives pictured in
Figure 2: (a) a
nonrotating core, that is,
 0 = 0,
and (b) a rotating
core,
0 = 0,
and (b) a rotating
core,  0
0
 0.
Suppose that some disturbance, such as tidal action, causes the ejection
from the core of a number of stars at P. The resulting orbits of
three stars, 1, 2, and 3, are schematically indicated in
Figure 2. For
0.
Suppose that some disturbance, such as tidal action, causes the ejection
from the core of a number of stars at P. The resulting orbits of
three stars, 1, 2, and 3, are schematically indicated in
Figure 2. For
 0
0
 0
distinct spiral arms may be formed, provided a sufficient number of
stars are ejected whose radial and tangential velocity components
vr
and vt relative to the core are in certain favorable
relations to the peripheral velocity r0
0
distinct spiral arms may be formed, provided a sufficient number of
stars are ejected whose radial and tangential velocity components
vr
and vt relative to the core are in certain favorable
relations to the peripheral velocity r0
 0 of the
core.
0 of the
core.

|
Figure 2. Rotation of nebulae and shape of spiral arms. |
It should be remarked that the orbits 1, 2, 3, etc., in Figure 2b are ellipses only if outside the core the corresponding masses are no longer acted upon by the forces which originally caused their ejection from the core. If, for example, the ejection is brought about by the close encounter of the nebula with another nebula, tidal actions will continue until the second nebula has moved far away and our simple model must be correspondingly modified. It may suffice here to point out that in addition to the creation of angular momentum in a nebula, a close encounter may also set up radial pulsation in this nebula. This pulsation will not, in general, be spherically symmetrical. As a first approximation we can schematically characterize it by what might be called the "tidal ellipsoid" or "ellipsoid of pulsation." The magnitudes and signs of the radial velocities which are induced along the principal axes of this ellipsoid by the passing second nebula approximately determine the character of the resulting pulsation in the nebula under consideration.
The probable existence of pulsation in many nebulae further complicates the interpretation of differences in the observed velocities Vs along the line of sight of various parts of a nebula. If we have pulsation, Vs differs from the value of Vt owing to rotation alone, by amounts which depend on the position of the tidal ellipsoid relative to the two vectors which define the line of sight and the axis of rotation. In two obvious, simple cases the functions Vs(r) may graphically assume the forms represented by the two dotted curves (Vs and Vs') in Figure 1.
The possible existence of pulsation also suggests that we cannot, without additional knowledge, interpret ellipsoidal shapes of nebulae as being due to rotation alone. Values of the masses of nebulae which are derived on the assumption that elliptical nebulae are stellar systems in rotational equilibrium must therefore be viewed with suspicion.
Before embarking on any detailed analysis of spiral structures it will be advisable to obtain first qualitative information concerning the shape of the spiral arms in relation to the sense of rotation of the core. Promising results in this direction have already been secured by Dr. W. Baade of the Mount Wilson Observatory, who has found that the tips of the spiral arms of the Andromeda nebula are curved in the direction determined by the sense of rotation of the core, as pictured in Figure 2b. I am indebted to Dr. Baade for a private communication of this unpublished result.
Summing up, we may say that present data on internal rotations furnish, at best, minimum values Mmin for the masses of the nebulae. Such minimum values are obtained if we assume that nebulae are stable systems whose components have velocities v inferior to the velocity of escape ve from the system. Therefore
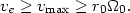
| (9) |
But
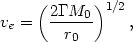
| (10) |
where M0, r0, and
 0 are the
mass, the radius, and the angular velocity
of the core. Consequently, the mass M of the nebula is
0 are the
mass, the radius, and the angular velocity
of the core. Consequently, the mass M of the nebula is
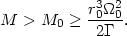
| (11) |
For example, in the case of NGC 4594 we have
r0  4.3
× 1021 cm and r0
4.3
× 1021 cm and r0
 0
0
 4 × 107
cm/sec, which gives
4 × 107
cm/sec, which gives
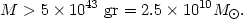
| (12) |
The data used are taken from the paper on NGC 4594 by F. G. Pease, (4) who, in 1916, measured the spectroscopic rotation of this nebula. Pease also was the first to point out that the central parts of nebulae rotate like solid bodies.
Since the determination of nebular masses is of considerable importance in modern astrophysics, three new methods for the solution of this problem are briefly outlined in the following pages. Two of these I have proposed already in previous communications. (5) ,(6). The third, in a restricted form, has been applied thus far only to clusters of stars. (7) Its applicability to clusters of nebulae remains to be investigated. The purpose of this paper is to discuss the basic principles on which the new methods rest.
3 Gaskugeln (Leipzig, 1907). Back.
4 Proc. Nat. Acad., 2, 517, 1916. Back.
5 F. Zwicky, Helv. physica acta, 6, 110, 1933. Back.
6 F. Zwicky, Phys. Rev., 51, 290, and 51, 679, 1937. Back.
7 H. von Zeipel, Jubilaeumsnummer d. A. N., p. 33, 1921. Back.