If the total masses of clusters of nebulae were known, the average masses of cluster nebulae could immediately be determined from counts of nebulae in these clusters, provided internebular material is of the same density inside and outside of clusters.
As a first approximation, it is probably legitimate to assume that clusters of nebulae such as the Coma cluster (see Fig. 3) are mechanically stationary systems. With this assumption, the virial theorem of classical mechanics gives the total mass of a cluster in terms of the average square of the velocities of the individual nebulae which constitute this cluster. (5) But even if we drop the assumption that clusters represent stationary configurations, the virial theorem, in conjunction with certain additional data, allows us to draw important conclusions concerning the masses of nebulae, as will now be shown.
|
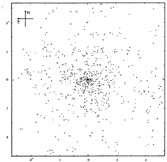
Figure 3. The Coma cluster of nebulae. |
Suppose that the radius vector from a fixed point in the cluster to
the nebula (
) of mass
M is
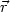
. For
the fixed point we conveniently
chose the center of mass of the whole cluster. The fundamental law
of motion of the nebula
() is
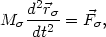
| (13) |
where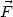 
is the total
force acting on M. Scalar multiplication of this equation with
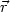
gives
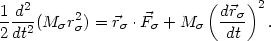
| (14) |
Summation over all the nebulae of the cluster leads to
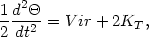
| (15) |
where 
=
M
r2 is the polar moment of inertia of the cluster,
Vir =
.
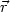
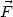
is the
virial of the cluster, and KT is the sum of the
kinetic energies of translation of the individual nebulae. If the cluster
under consideration is stationary, its polar moment of inertia
fluctuates around a constant value
0, such
that the time average
of its derivatives with respect to time is zero. Denoting time averages
by a bar, we have in this case
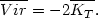
| (16) |
On the assumption that Newton's inverse square law accurately describes the gravitational interactions among nebulae, it follows that
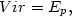
| (17) |
where
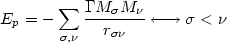
| (18) |
is the total potential energy of the cluster due to the gravitational interactions of its member nebulae. Equation (16) thus takes on the well-known form
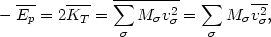
| (19) |
where v is
the velocity of the mass
M. In
order to arrive at a quantitative estimate of the total mass
of a globular cluster
of nebulae,
we assume as a first approximation that these nebulae are, on the
average, uniformly distributed inside a sphere of radius R. In this
case
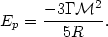
| (20) |
We may also write
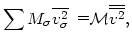
| (21) |
where the double bar indicates a double average taken over time and over mass. Therefore, from (19), (20), and (21),
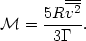
| (22) |
This relation (22) can also be derived if we take the time average
of equation (14) which holds for an individual nebula. The time
average of the left side of (14) disappears if the mass
M is
a member of a stationary system. Thus we have
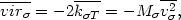
| (23) |
where
vir is the virial
of the nebula () and
kT is
its kinetic energy. Now, in a sphere of mass
and radius R,
the density
, if uniform,
is equal to
=
3 /
4
R3. The force
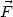
(r) which acts
on M
is therefore
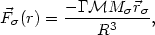
| (24) |
and the virial
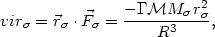
| (25) |
which, combined with (23), results in
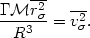
| (26) |
Since it has been assumed that all the nebulae combined produce a uniform distribution of matter throughout the sphere, the average nebula spends equal times in equal volumes, and we have
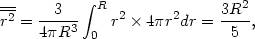
| (27) |
where the double bar again designates a double average with respect to time and mass. Consequently,
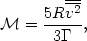
| (28) |
as before.
From the distribution of the brighter nebulae in the Coma cluster
pictured in Figure 3 it is apparent that the
assumption of uniform
distribution is not fulfilled. But it is also evident that the actual
potential energy Ep will have a value which, in order
of magnitude,
is correctly given by (20). Even if we crowded all the cluster nebulae
into a sphere of radius R/2, the value of Ep
would only be doubled.
Also, we can increase Ep only very little if we assume
that the
M's
run through a wide range of values. For instance, if we assumed that
practically the whole mass
of the cluster were
concentrated in only two or three nebulae of mass
/ 2 or
/ 3,
respectively, and
that these masses had mutual distances as small as R/10, we should
arrive at values for the potential energy:
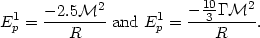
| (29) |
These values are of the same order of magnitude as in (20). The
following inequalities must therefore be considered as conservative
estimates for the possible maximum values of the average kinetic
energy and the minimum values of the total mass
:
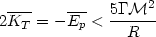
| (30) |
and
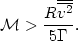
| (31) |
We apply this relation to the Coma cluster of nebulae whose radius is of the order of 2 × 106 light-years. From the observational data we do not know directly the velocities v of the individual nebulae relative to the center of mass of the cluster. Only the velocity components vs along the line of sight from the observer are known from the observed spectra of cluster nebulae. For a velocity distribution of spherical symmetry, however, we have
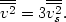
| (32) |
Therefore
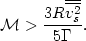
| (33) |
From the observations of the Coma cluster so far available we have, approximately, (5)
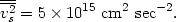
| (34) |
This average has been calculated as an average of the velocity
squares alone without assigning to them any mass weights, as actually
should be done according to (21). It seems, however, as Sinclair
Smith (8)
has shown for the Virgo cluster, that the velocity dispersion
for bright nebulae is about the same as that for faint nebulae.
Assuming this to be true also for the Coma cluster, it follows that the
mass-weighted means of v2 and the straight means are
essentially the
same. Furthermore, in calculating (34) we have used velocities
which belong to the bright nebulae, since only these have been measured.
If brightness can be taken as a qualitative indication of mass,
the error in substituting (34) for (21) cannot be great. We must,
nevertheless, remember that, strictly speaking, the determination of
by the virial theorem
is subject to the difficulty of
calculating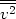 
through the application of an averaging process which involves the
as yet unknown masses. The mass
, as obtained from the
virial theorem, can therefore be regarded as correct only in order of
magnitude.
Combining (33) and (34), we find
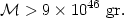
| (35) |
The Coma cluster contains about one thousand nebulae. The average mass of one of these nebulae is therefore
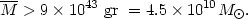
| (36) |
Inasmuch as we have introduced at every step of our argument
inequalities which tend to depress the final value of the mass
, the
foregoing value (36) should be considered as the lowest estimate for
the average mass of nebulae in the Coma cluster. This result is
somewhat unexpected, in view of the fact that the luminosity of an
average nebula is equal to that of about
8.5 × 107 suns. According to (36), the conversion factor
from
luminosity to mass for nebulae in the Coma cluster would be of the order
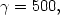
| (37) |
as compared with about
' = 3 for
the local Kapteyn stellar system.
This discrepancy is so great that a further analysis of the problem
is in order. Parts of the following discussion were published several
years ago, when the conclusion expressed in (36) was reached for the
first time. (5)
We inquire first what happens if the cluster considered is not stationary, in which case the virial theorem (16) must be replaced by one of the two inequalities
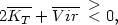
| (38) |
where the bars denote averages taken over time intervals which are comparable with the time it takes one nebula to traverse the whole system. The smaller sign needs no further consideration, since instead of resulting in equation (19) it leads to the inequality
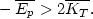
| (39) |
This, in turn, means that the inequality (33) is further enhanced,
and we arrive at a lowest value for the mass
greater even than (36).
The other alternative is
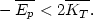
| (40) |
We may combine this inequality with the principle of conservation of total energy E of the whole cluster
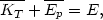
| (41) |
which, added to (40), leads to
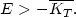
| (42) |
This means that the cluster is expanding. In particular, if E = 0 we have
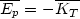
| (43) |
instead of
=
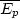-2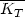
, for
a stationary system. Equation (43)
means that the cluster will ultimately just fly apart. In this case the
mass of the cluster
still has a value of half that arrived at in (36),
and the discrepancy between the conversion factors
and
' remains
materially the same in order of magnitude.
If we wish to reduce the mass
sti1l further so as
to make approximately
=
', we must
put E > 0 and
KT >> - Ep. By
assuming this, however, we run into two serious difficulties. In the
first place, it is difficult to understand why under these circumstances
there are any great clusters of nebulae remaining in existence at all,
since the formation of great clusters by purely geometrical chance is
vanishingly small, as will be shown in another paper. In the second
place, the cluster nebulae, after complete dispersion of a cluster
would still possess velocities practically identical with their original
velocities. The field nebulae in general, which under the assumed
circumstances can hardly have a velocity distribution different from
that of former cluster nebulae, should therefore have a dispersion in
peculiar velocities comparable to that of cluster nebulae. The average
range of peculiar velocities among field nebulae, however, seems
to be of the order of 150 km/sec only. This observation, if correct,
excludes values of the total energy E which are sufficiently greater
than zero to reduce the discrepancy between
and
' to a
satisfactory
degree. (5) It will,
nevertheless, be advisable to obtain more data
on the velocities of both cluster nebulae and field nebulae in order
to arrive at accurate values of the dispersion which characterizes the
respective velocity distribution functions.
In addition it will be necessary to develop methods which allow us to determine the relative amounts of internebular material in clusters as well as in the general field.
It should also be noticed that the virial theorem as applied to clusters of nebulae provides for a test of the validity of the inverse square law of gravitational forces. This is of fundamental interest because of the enormous distances which separate the gravitating bodies whose motions are investigated. Since clusters of nebulae are the largest known aggregations of matter, the study of their mechanical behavior forms the last stepping-stone before we approach the investigation of the universe as a whole.
The result (36) taken at face value of course does not mean that the average masses of field nebulae must be as great as those of cluster nebulae. From the general principles discussed in a following section one would rather expect the heaviest nebulae to be favored in the process of clustering.
The distribution of nebulae in the Coma cluster, illustrated in Figure 3, rather suggests that stationary conditions prevail in this cluster. It is proposed, therefore, to study the Coma cluster in more detail. On the other hand, the virial theorem can hardly be used with much confidence in cases such as the Virgo cluster and the Pisces cluster. (9) These clusters are much more open and asymmetrical than the Coma cluster and their boundaries are thus far ill defined. Accurate values of the gravitational potentials in these clusters are difficult to determine.
In passing it should be noted that the mechanical conditions in clusters of nebulae are in some important respects different from the conditions in clusters of stars. During close encounters of stars only a minute part of their translational energy is transformed into internal energy of these stars, if the extremely rare cases of actual impacts are disregarded. Nebulae act differently, In the first place, close encounters and actual impacts in a cluster of nebulae must occur during time intervals which are not very long compared with the time of passage of one nebula through the entire system. Therefore, a considerable tendency exists toward equipartition of rotational and internal energy of nebulae with their translational energy. Star clusters in some ways are analogous to gas spheres built up of monatomic gases, whereas clusters of nebulae may be likened to gas spheres built up of polyatomic gases. This difference in internal characteristics may lead ultimately to serious consequences, as will be seen from the following line of reasoning.
We again start from the virial theorem (19), in the form in which it may be written for stationary gravitational systems, namely,
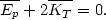
| (44) |
Admitting that on close encounters of nebulae kinetic energy of translation KT may be transformed into energy of rotation KR and internal energy EI of nebulae, we must replace the restricted form (41) of the energy principle by the more general equation
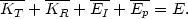
| (45) |
Combining (44) and (45), we have
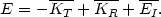
| (46) |
Encounters among nebulae tend to establish equipartition among translational, rotational, and internal energies of nebulae, analogous to the equipartition of energy among different degrees of freedom which is so well known in ordinary statistical mechanics. The mechanical conditions in a cluster of nebulae should converge toward a state for which
| (47) |
where
> 0. For instance,
= 1 if we include in
EI only the kinetic
energy of the first three fundamental modes of pulsation of the whole
system. The older the system becomes, the more of its many degrees
of freedom may be expected to share in the equipartition of
energy. Other happenings excluded, the value of
would, therefore,
increase almost indefinitely as the average value
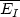of
EI is determined
for time intervals of increasing length. In any case, admitting (47),
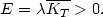
| (48) |
We are thus led to the uncomfortable conclusion that the total energy of a stationary cluster of nebulae should be positive, This is a contradiction in itself, since it means that on the assumption of stationary conditions in a cluster we have proved that the cluster really cannot be stationary but must ultimately fly apart. It would seem, therefore, that clusters of nebulae analogous to gravitational gas spheres 3 which are built up of polyatomic gases could never represent stationary configurations. In reality, however, condition (47) cannot be reached. In contradistinction to the rotational energy of polyatomic molecules at low temperatures, the rotational energy kR of a nebula cannot become equal to its observed translational energy kT. Long before the equipartition (47) among the various types of energy can be established by close encounters among nebulae, these nebulae will have been partially or completely disrupted. We are here confronted with processes which are analogous to the dissociation of polyatomic molecules when their average kinetic energy of translation - that is, the temperature of the gas - becomes too high.
The preceding considerations open up interesting new vistas on the change in time of nebular types in clusters where close encounters are much more frequent than among field nebulae. In the first place, the most compact and most massive nebulae are presumably the least vulnerable to disruption. These nebulae, therefore, are destined to survive the longest. This effect of selective elimination of nebular types may, in part, be responsible for the difference in the representation of types among cluster nebulae as compared with field nebulae. In the second place, we should. expect a considerable number of stars, as well as matter in dispersed form from disrupted nebulae, to be scattered through the internebular spaces within clusters. Sufficiently large amounts of internebular matter in clusters might seriously change our estimate (36) of the average value of nebular masses as derived from the preceding application of the virial theorem to clusters of nebulae. It is therefore the intention to undertake a series of observations which may throw some light on the problem of the density of internebular matter in clusters, as compared with the density of matter in the general field. Until such observations have been made it will be well to keep in mind that, although the determination of average nebular masses from the virial theorem may be viewed with considerable confidence, this method is not entirely free from objections which have not yet been satisfactorily dealt with.
In principle the virial theorem may also be applied to describe the mechanical conditions in an individual nebula. Actually a direct application is difficult, since it is not possible to measure separately, as in the case of a cluster of nebulae, the velocities of the individual units of mass which constitute a nebula. The average square velocity (21) might be derived from the shape of the spectral lines in the light from nebulae. Unfortunately, the practical determination of such shapes is at present exceedingly difficult, if not impossible. In addition the spectral lines in the light of nebulae are doubtless of complex origin, and the interpretation even of well-known shapes of lines is by no means an easy task.
9 F. Zwicky, Proc. Nat. Acad., May, 1937. Back