It will be shown elsewhere that the number of clusters of nebulae actually observed is far greater than the number that might be expected for a random distribution of non-interacting objects. This tendency of nebulae toward clustering is no doubt due to the action of gravitational forces.
By a bold extrapolation of well-known results of ordinary statistical mechanics we adopt the following working hypothesis as a tentative basis for the interpretation of future observations on the clustering of nebulae.
BASIC PRINCIPLES
1. The system of extragalactic nebulae throughout the known parts of the universe forms a statistically stationary system.
2. Every constellation of nebulae is to be endowed with a probability
weight
f (
) which is
a function of the total energy
of this
constellation. Quantitatively the probability P of the occurrence
of a certain configuration of nebulae is assumed to be of the type
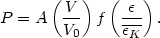
| (49) |
Here V is the volume occupied by the configuration or cluster
considered, V0 is the volume to be allotted, on the
average, to any
individual nebula in the known parts of the universe, and
is
the total energy of the cluster in question, while
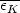will probably be found to
be proportional to the average kinetic energy of individual nebulae.
The function A(V / V0) can be determined
a priori. On the other hand,
f ( /
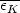) presumably will be found to be
a monotonously decreasing function in
/
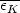, analogous in type to a Boltzmann factor
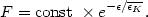
| (50) |
Assuming the basic principles stated in the preceding to be correct, we may draw the following hypothetical conclusions:
a) The clustering of nebulae is favored by high values of f and is partially checked by low values of the a priori probability A.
b) If, as would appear to be certain, nebulae are not all of the same mass, nebulae of high mass are favored in the process of clustering, since they contribute most to produce high values of the weight function f.
c) As a consequence of b, we should expect that the frequency with which different types of nebulae occur will not be the same among field nebulae and among cluster nebulae. In other words, clustering is a process which tends to segregate certain types of nebulae from the remaining types. This may contribute toward the correct interpretation of the well-known fact that cluster nebulae are preponderantly of the globular and elliptical types, whereas field nebulae are mostly spirals. From the arguments put forth in the preceding section as well as in section iii it follows that it is not necessary as yet to call on evolutionary processes to explain why the representation of nebular types in clusters differs from that in the general field. Here, as in the interpretation of other astronomical phenomena, the idea of evolution may have been called upon prematurely. It cannot be overemphasized in this connection that systematic and irreversible evolutionary changes in the domain of astronomy have thus far in no case been definitely established.
d) If cluster nebulae, on the average, are really more massive than field nebulae, the conclusion suggests itself that globular nebulae may, somewhat unexpectedly, be among the most massive systems. It will be of great interest to check this inference by a search for gravitational lens effects among globular nebulae.
The preceding considerations point toward the possibility of an entirely new approach in the study of masses of nebulae. We may argue somewhat as follows:
The function A(V / V0), as said before,
can be obtained from the
theory of probabilities applied to random distributions in space of
non-interacting objects. The function A, therefore, is known a
priori. The function f may be determined from counts of types of
clusters of nebulae (single, double, triple, quadruple nebulae, etc.) in
given volumes of space. Such counts will give directly the values of
P characteristic for different clusters. The
numerical values of the
function f follow from f = P / A. In order
to determine the masses of individual nebulae, we must express the argument
/
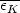of the
function f in terms of these masses and then seek to correlate each
definite argument with one numerical value of f. To solve this
problem of the functional form off we may proceed as follows:
We first segregate the nebulae into classes of types
T1, T2, T3,
. . . Tn. For these types the usual ones,
E0, E1, . . . E7,
Sa, Sb, Sc, etc.,
may, for instance, be chosen. As a first approximation we assume
tentatively that the mass
M
(L) of a nebula of a given type
T is a
function of its luminosity L alone. The argument
/
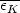of the
function f may then be formulated mathematically in terms of
M,
r
and v,
where the
M are
the unknown masses of the various types
(T) of
nebulae in the cluster and where the velocities
v of
these nebulae, as well as their mutual distances
r
, are known from
observation. Since the numerical values of f are already known, the
functional dependence of these values on the arguments
/
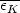can
then be determined by a purely mathematical procedure. Once the
form of the function
f ( /
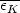) is known, the
unknown masses follow from our knowledge of
/
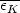expressed in terms of
M,
v,
r
. It
should be noted, however, that the method just described gives only
relative masses
M /
M0, measured, for instance, with the mass
M0
of the type T0 taken as the arbitrary unit. Only if
the absolute value of
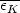is known or if we have independent knowledge
of M0 can we derive the absolute values
M from
the statistics of nebular distribution.
Needless to say, this program, if it can be carried out, provides the most powerful method of determining the masses of all types of nebulae. In addition, it also enables us to determine the statistical weights f. The practical application of this method necessitates a great amount of observational work. In view of this fact, it will perhaps be advantageous to apply the preceding program first in a restricted form by a consideration of the distribution of various types of nebulae in one individual great cluster. The procedure to be applied in this case is analogous to that used successfully by H. von Zeipel 7 in his determination of the masses of different types of stars in certain clusters of stars.
Since it is intended to carry out the investigation just mentioned on the Coma cluster, a few preliminary remarks concerning the distribution of nebulae in this cluster are here given.