5.2. Types of Interaction Between Galaxies in Pairs

Vorontsov-Vel'yaminov (1955, 1977) and Arp (1966) presented a large number of interacting systems of galaxies, of which a considerable number are pairs. The forms of the interactions are so multi-patterned that Vorontsov-Vel'yaminov turned to zoological language: mice, anteaters, spiders, cuttlefish, etc. The zoo of unusual systems was later extended to objects in the southern sky (Bergvall, 1981a, b, Arp and Madore, 1989). After some early attempts to explain these unusual structures by non-gravitational forces or magnetic effects a more systematic approach was taken, using numerical modelling. Toomre and Toomre (1972) Clutton-Brock (1972), and Eneev et al. (1973) showed that models with large numbers of particles moving in the field of a central massive object and affected by the gravitational influence of another massive galaxy can explain many of the connections, tails, and other observed properties of interacting galaxies. For some well-studied systems (M51, NGC 4038 / 4039) it has proved possible to model not only the peculiar forms of the objects but also their entire velocity fields.

In order to seek any general relations, such as might characterize the forms of interaction, for example, or relate the forms of interaction and the structural types, it was necessary to introduce a rather simple classification scheme. The detailed descriptions of objects in the Vorontsov-Vel'yaminov Atlases (1959, 1977) and in the MCG catalogue are unsuitable for this purpose ⁽⁵⁾ , and so we introduced a simpler classification along the lines presented in figure 3. In this scheme we included the following criteria: a) the type of interaction should be unique; b) it is desirable that the description depend as little as possible on the separation and the orientation angle with respect to the line of sight; c) every interaction class should contain a substantial number of objects. The basic notions behind each of these classifications may be simply listed.

The first type, LIN, includes double systems with observed linear structures with the appearance of a bridge (br), tail (ta) or both (br+ta). The second type, ATM, includes pairs with components surrounded by a common single atmosphere, additionally described as having amorphous symmetry (am) or irregular shell-like structure, (sh). The last type, DIS, covers the cases in which no intergalactic medium is visible around the double system, but interactions appear to have severely distorted the forms of one (1) or both (2) components of the pair (see figure 3).

We carried out the classification of interaction types on charts from the Palomar Atlas. The modest scale of these charts (67"/mm), and the over-exposure of the central regions of galaxies, did not always allow a secure estimate. For the double systems in the catalogue which were detected radio sources, Stocke et al. (1978) obtained images of these pairs at a scale of 10"/mm and classified the interaction type anew, changing the classification for about 16% of the pairs. To establish properly the forms of interaction of pairs of galaxies (as well as the structural types for the components) it is always important to have a large scale atlas of these simple systems, in which a large fraction of the cases manifest the process of mutual gravitational influence.

Among the 487 catalogue pairs with f < 100 there are signs of interaction visible for 59%. Figure 35 shows how the relative numbers of interacting pairs Q_int changes with the projected linear separation between components. The vertical bars indicate the standard deviation of the sample values. Within the statistical errors, Q_int decreases monotonically with increasing separation and falls to zero for X > 110 kpc. This critical value X = 110 kpc may be viewed as the maximal range at which apparent signs of interaction can be produced.

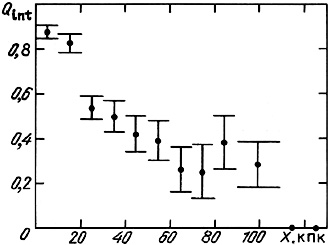Figure 35.

In the preceding paragraphs we noted that double galaxies with both components of the same morphological type are encountered much more often than for chance combinations. This trend continues more strongly for interacting pairs. Figure 36 shows values of the Hubble type correlation function for double systems calculated according to (5.1). Diamonds indicate the data for interacting pairs, and, as usual, the height of the diamonds indicates the standard deviation. The points with vertical error bars indicate the analogous quantities for non-interacting systems. As we see, the excess number of matched pairs is larger for the interacting systems. One might first suppose that this difference is due to changes in the structure of the galaxies produced by their mutual tidal forces. However, we know (see figure 33) that the amplitude (0) depends on the separation between components, and since interacting pairs are on the whole much tighter systems than the average, the excess of common morphological types may be explained as a separation effect. Quantitative analysis of pairs including distribution effects indicates a preference for this explanation.

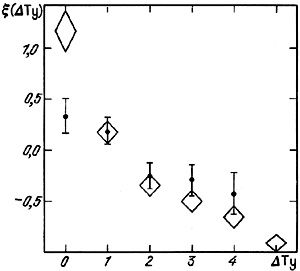Figure 36.

For understanding the properties of the interactions of galaxies in pairs, an important consideration is the relation between the various structural types of galaxies in each class of interaction. We have not encountered any previous systematic approach to this in the literature, so as a start we present such data in Table 18, including the percentage of the indicated Hubble types of galaxies broken down according to each interaction class. Double systems with no indications of interaction are marked N/I. In parentheses are given the total numbers of galaxies involved.

It follows from these data that the distribution of early and late galaxy types among various interaction classes is very uneven. Elliptical galaxies are encountered only rarely among systems with bridges and tails. By contrast, in pairs surrounded with amorphous atmospheres elliptical objects represent a 91% majority. Apparently, thin (one-dimensional) structures are gravitationally induced in those galaxies which contain a disk with predominantly circular stellar motions. Interactions in galaxies with spherical forms and characteristically almost radial stellar orbits give rise preferentially to amorphous atmospheres. This dependence of the width of the structures produced by interactions on the stellar velocity dispersion in galaxies was discussed by Clutton-Brock (1972), on the basis of model calculations. Confirmation of this notion would come from detailed measurements of the colours of bridges, tails, and atmospheres around double galaxies. Unfortunately, such observations are still very sparse. NOTE: Not so sparse any more.

Among the various properties of the distribution of interacting pairs according to structural type of the components we may remark the following: a) systems with shell-like asymmetric atmospheres contain a substantially higher percentage of spirals than do those with amorphous atmospheres; b) double galaxies with disturbed forms for one or both components include predominantly spiral objects; c) the morphological distribution of non-interacting pairs is substantially the same as the mean for all interacting pairs; in other words, galaxies of a given Hubble type have about the same chance of showing signs of interaction ⁽⁶⁾ .

The forms of disturbance in double systems may depend not only on the dominant type of stellar motion in their components but also on the luminosity and size of the galaxies, the orbital eccentricity, the orientation of the spin axis of the galaxies in relation to the orbital angular momentum, and other parameters. A proper exploration and explanation of such tendencies is still awaited, but we can note a few basic tendencies. Table 19 presents the mean values of the following quantities for each type of interaction: the absolute value of the radial velocity difference <y>, the projected linear separation between components <X>, the total pair luminosity <L₁₂>, and the orbital mass-to-luminosity ratio <f_c> corrected for radial velocity errors. Each mean is accompanied by its standard deviation. Comparison of these quantities illustrates the following properties.

In chapter 3 we presented data strongly arguing that pairs of galaxies with f > 100 are not in fact isolated physical systems. However, among the 98 double systems in the catalogue excluded from further analysis on these grounds, 28 are classified in the catalogue as interacting. This clearly deserves further discussion and clarification. All 28 interacting pairs with f > 100 were so classified on charts of the Palomar Atlas and found to show signs of interaction, but in the majority of these cases the signs were vague or very general. In 15 cases the signs were present in only one component (D(1)). In fact, they may also be attributable to chance asymmetries in the spiral patterns of galaxies, or even disturbances in the general form of galaxies due to projected foreground stars. Only 6 systems appear as interacting according to Arp (1966) or Vorontsov-Vel'yaminov (1959, 1977): number 305 = VV 218; number 396 = VV 317; number 427 = VV 458 = Arp 274; number 481 = VV 220 = Arp 272; number 483 = VV 215; and number 586 = VV 314 = Arp 46. In two cases (numbers 427 and 586), one component of the pair shows a possible interaction with a compact companion, itself having a small difference in radial velocity. Double galaxies numbers 481 and 483 are located in the central region of the rich cluster in Hercules where the probability of chance projection of galaxies is rather high. In the contact pairs numbers 305 and 396 the signs of interaction are particularly vague. Therefore, among double systems with f > 100 we have not found a single example of a definite physical connection between galaxies with large differences in radial velocity.

⁵ The many interacting systems in the MCG are described in very general and memorable words. For example: "4-6-42. Two branches extending next to each other like a cow's horns, and, on the opposite side, a long tail", "3-1-2. The appearance of a night cap littered with points", "-1-5-43. The form looks like the lower part of a person bending over holding a ball between his knees". Back.

⁶ The small number of Sm galaxies among non-interacting pairs follows from the effect of the isolation criterion, which discriminates against wide pairs containing objects of low luminosity. Back.