6.2. The Spatial Distribution of Pairs

Ignoring the a priori isolation of double galaxies from their nearest neighbours, many pairs are found in systems of higher multiplicity. The isolated galaxy pairs delineate a picture of multi-stage clustering, and therefore the distribution of pair centers maintains `frozen' information about the formation conditions of the observed hierarchy.

Inspecting the distribution of double galaxies by apparent magnitude (figure 12) and radial velocity (figure 14), we noted that a significant fraction of bright pairs are in the Local Supercluster. We illustrate this in figure 42, which shows the distribution of bright pairs in supergalactic latitude (SGB). The cross hatching indicates objects with radial velocity less than 2500 km/s. Galaxies with greater velocities are located beyond the limits of the Local Supercluster. The closer pairs exhibit a markedly greater concentration to the super-galactic equator, with an rms latitude of <SGB²>^1/2 = 24° ± 3°, whereas for the entire sample it is 32° ± 1°. The distributions N(SGB) and N(V₀) allow us to conclude that about half of the double systems with V₀ < 2500 km/s are in fact members of the Local Supercluster.

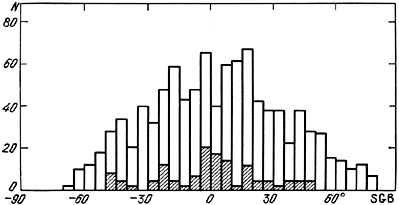Figure 42.

The overall distribution of pair centers on the sky in equatorial coordinates (, ) was shown in figure 4, where we see significant non-uniformities. However, the known nearby clusters of galaxies are not present with the same high contrast as the distribution of all galaxies from the CGCG to the same limiting magnitude.

Karachentsev and Shcherbanovsky (1983) examined the spatial distribution of double systems on a variety of scales. The distance of pairs of galaxies from the observer was calculated from the mean radial velocity of the components for a Hubble constant H = 75 km/s/Mpc. For each pair, its distance from the nearest five double systems was calculated to evaluate the role of chance groupings of pairs.

The distribution of pairs according to separation from the nearest neighbour has a maximum at 5 Mpc. Among 487 pairs only the 19 nearest neighbours are closer than 2 Mpc, and 7 are closer than 1 Mpc. About 80% of such cases are in the region of the Local Supercluster. Using the index of galaxy groups by de Vaucouleurs (1975) it is easy to convince oneself that almost all pairs which have such close neighbour pairs are in fact members of these groups (or even the Virgo cluster). In only one case do two pairs of galaxies, numbers 195 and 199, form an apparently isolated binary system of pairs, with projected separation 0.92 Mpc. Therefore, analysis of the three-dimensional distribution of pair centers establishes that the features of their small-scale distribution are due not to individual associations of the "pair + pair pair", type, but to the membership of double galaxies in the population of groups and clusters.

Besides the concentrations to the nearest groups and the Local Supercluster, double galaxies show some distribution properties with respect to the contours of other known superclusters, such as those in Perseus, Coma and Hercules. This tendency was demonstrated by Tifft (1980) on sky maps in which the distribution of double galaxies was projected in fixed intervals of radial velocity. This claim about the large-scale distribution of pair centers is shown in the form of a `pie' diagram in figure 43, which shows objects with V₀ < 10000 km/s in the region 9^h < < 17^h, 0° < < 20°. The Local Supercluster has a radial appearance in this diagram due to its virial motions. In the radial velocity interval shown here, the southern part of the Coma supercluster is noticeable near V₀ = 7000 km/s and = 13.5^h. Between this and the Local Supercluster is a known empty region which was detected from field galaxies. Comparison of figure 43 with the analogous diagram in Davis et al. (1982) for galaxies brighter than magnitude 14.5 shows a noteworthy general agreement for voids and groups. However, an unmistakable characteristic of the distribution of pairs is the weaker concentration of objects to the densest regions of clusters.

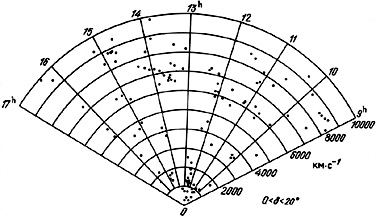Figure 43.

For a quantitative estimate of the differences in the spatial distributions of galaxies and the centers of pairs, we calculated the two-point correlation function (r) and compared it to the data presented by Peebles (1980). From our subsample we excluded the zone of low galactic latitude with | b| < 30° and the distant objects with V₀ > 7500 km/s. This refinement of the sample was dictated by the need to reduce the effects of non-uniformity due to galactic absorption and of selection effects in the distance from the observer. The correlation function per unit steradian was calculated for a range extending to D = 100 Mpc. A selective decline in (r) due to the boundaries of the region was avoided by excluding pairs located within b = 6° and = 6° from the perimeter.

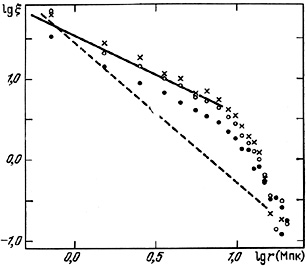Figure 44.

The calculated (r) for the centers of pairs is shown in figure 44. The filled circles indicate values of the correlation function of pairs with V₀ < 7500 km/s, the open circles are for pairs with V₀ < 5000 km/s, and the crosses are for V₀ < 2500 km/s. The last subsample is dominated by the Local Supercluster. Statistically significant values of the two-point correlation function were measured on scales from 0.7 to 20 Mpc. In the range 0.7 to 8 Mpc the correlation function is well fit by

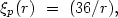(6.4)

and for r > 10 Mpc it falls as r^-5. The dashed line indicates the function

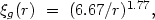(6.5)

found by Peebles (1980) for galaxies in the Zwicky catalogue, scaled to H = 75 km/s/Mpc over the interval 130 kpc to 13 Mpc.

As the range of V₀, i.e., the sample depth, is reduced, the sample completeness increases. Along with this the amplitude of _p(r) rises but its slope remains practically unchanged. For all examined intervals the amplitude of the spatial distribution function (r) for double systems is higher than it is for galaxies. An analogous effect was demonstrated by Klypin and Kopilov (1983) for the correlation function of clusters of galaxies.

With regard to the various limitations on _p and _g, the question arises as to whether it is possible for these differences to have been introduced by the action of the isolation criteria. The mean separation between members of pairs is <r₁₂> 50 kpc. According to the strict isolation criterion, no neighbour should occur in a zone of avoidance of size ~ 10<r₁₂> 0.5 Mpc. This characteristic length lies outside the intervals for which we have evaluated the correlation function, so that the selection criteria cannot have had a significant effect on the slope log_p(r).

Besides the effect of selection, another systematic difference between _p and _g may be an actual lack (or deficit) of double systems in the densest regions of groups and clusters, if wide pairs are exposed to disruption by tidal forces. It is not possible to exclude the idea that double systems formed in relatively sparse regions around the development of large-scale inhomogeneities which joined to the dense regions and are observed now as shells around rich clusters of galaxies. This could indeed explain the property that the maximum excess of _p over _g occurs on scales ~ 10 Mpc, in agreement with the typical radius of a supercluster.

The nature of the differences in the slope and amplitude of the correlation functions _p and _g will require further analysis. One stage would be investigating the spatial cross-correlation function _pg(r) between galaxies and the centers of pairs.